Question Number 26143 by chantriachheang last updated on 21/Dec/17
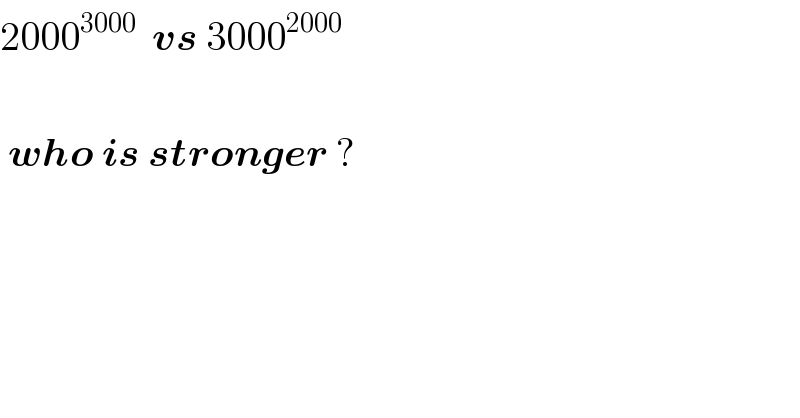
$$\mathrm{2000}^{\mathrm{3000}} \:\:\boldsymbol{{vs}}\:\mathrm{3000}^{\mathrm{2000}} \\ $$$$ \\ $$$$\:\boldsymbol{{who}}\:\boldsymbol{{is}}\:\boldsymbol{{stronger}}\:? \\ $$
Commented by Tinkutara last updated on 22/Dec/17
You can look at my question number 21781. Also this link is helpful: https://artofproblemsolving.com/community/c4h1522793
Answered by ajfour last updated on 21/Dec/17
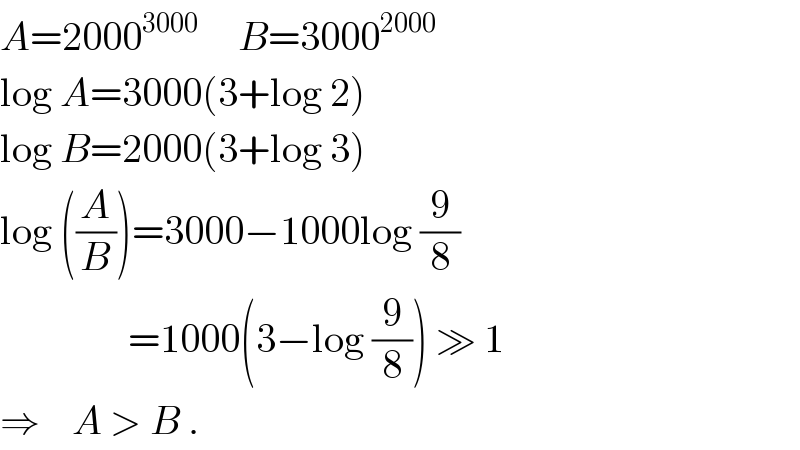
$${A}=\mathrm{2000}^{\mathrm{3000}} \:\:\:\:\:{B}=\mathrm{3000}^{\mathrm{2000}} \\ $$$$\mathrm{log}\:{A}=\mathrm{3000}\left(\mathrm{3}+\mathrm{log}\:\mathrm{2}\right) \\ $$$$\mathrm{log}\:{B}=\mathrm{2000}\left(\mathrm{3}+\mathrm{log}\:\mathrm{3}\right) \\ $$$$\mathrm{log}\:\left(\frac{{A}}{{B}}\right)=\mathrm{3000}−\mathrm{1000log}\:\frac{\mathrm{9}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1000}\left(\mathrm{3}−\mathrm{log}\:\frac{\mathrm{9}}{\mathrm{8}}\right)\:\gg\:\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:{A}\:>\:{B}\:. \\ $$
Answered by mrW1 last updated on 22/Dec/17
![((2000^(3000) )/(3000^(2000) ))=2000^(1000) ×((2000^(2000) )/(3000^(2000) )) =2000^(1000) ×((2/3))^(2000) =2000^(1000) ×[((2/3))^2 ]^(1000) =2000^(1000) ×[(4/9)]^(1000) =[2000×(4/9)]^(1000) ≈1000^(1000) =10^(3000) =100000...00_(3000 zeros) ⇒2000^(3000) is much much bigger than 3000^(2000) .](https://www.tinkutara.com/question/Q26190.png)
$$\frac{\mathrm{2000}^{\mathrm{3000}} }{\mathrm{3000}^{\mathrm{2000}} }=\mathrm{2000}^{\mathrm{1000}} ×\frac{\mathrm{2000}^{\mathrm{2000}} }{\mathrm{3000}^{\mathrm{2000}} } \\ $$$$=\mathrm{2000}^{\mathrm{1000}} ×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2000}} \\ $$$$=\mathrm{2000}^{\mathrm{1000}} ×\left[\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} \right]^{\mathrm{1000}} \\ $$$$=\mathrm{2000}^{\mathrm{1000}} ×\left[\frac{\mathrm{4}}{\mathrm{9}}\right]^{\mathrm{1000}} \\ $$$$=\left[\mathrm{2000}×\frac{\mathrm{4}}{\mathrm{9}}\right]^{\mathrm{1000}} \\ $$$$\approx\mathrm{1000}^{\mathrm{1000}} =\mathrm{10}^{\mathrm{3000}} =\mathrm{1}\underset{\mathrm{3000}\:{zeros}} {\mathrm{00000}…\mathrm{00}} \\ $$$$\Rightarrow\mathrm{2000}^{\mathrm{3000}} \:{is}\:{much}\:{much}\:{bigger}\:{than}\:\mathrm{3000}^{\mathrm{2000}} . \\ $$
