Question Number 118810 by greg_ed last updated on 19/Oct/20
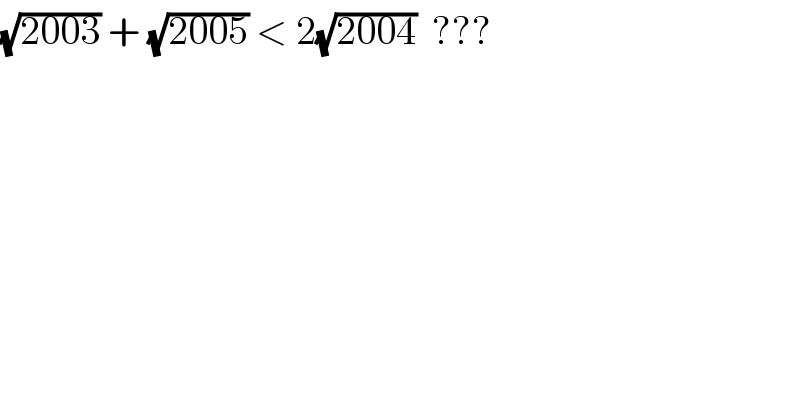
$$\sqrt{\mathrm{2003}}\:+\:\sqrt{\mathrm{2005}}\:<\:\mathrm{2}\sqrt{\mathrm{2004}}\:\:??? \\ $$
Answered by Olaf last updated on 19/Oct/20
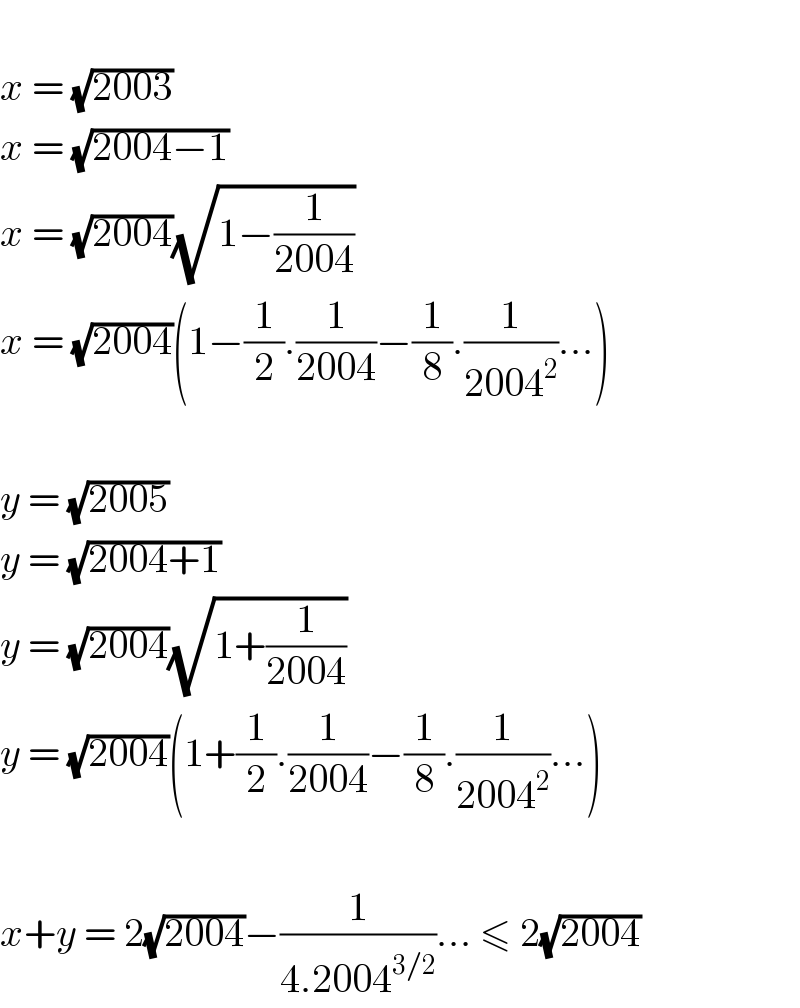
$$ \\ $$$${x}\:=\:\sqrt{\mathrm{2003}} \\ $$$${x}\:=\:\sqrt{\mathrm{2004}−\mathrm{1}} \\ $$$${x}\:=\:\sqrt{\mathrm{2004}}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2004}}} \\ $$$${x}\:=\:\sqrt{\mathrm{2004}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2004}}−\frac{\mathrm{1}}{\mathrm{8}}.\frac{\mathrm{1}}{\mathrm{2004}^{\mathrm{2}} }…\right) \\ $$$$ \\ $$$${y}\:=\:\sqrt{\mathrm{2005}} \\ $$$${y}\:=\:\sqrt{\mathrm{2004}+\mathrm{1}} \\ $$$${y}\:=\:\sqrt{\mathrm{2004}}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2004}}} \\ $$$${y}\:=\:\sqrt{\mathrm{2004}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2004}}−\frac{\mathrm{1}}{\mathrm{8}}.\frac{\mathrm{1}}{\mathrm{2004}^{\mathrm{2}} }…\right) \\ $$$$ \\ $$$${x}+{y}\:=\:\mathrm{2}\sqrt{\mathrm{2004}}−\frac{\mathrm{1}}{\mathrm{4}.\mathrm{2004}^{\mathrm{3}/\mathrm{2}} }…\:\leqslant\:\mathrm{2}\sqrt{\mathrm{2004}} \\ $$
Commented by greg_ed last updated on 20/Oct/20

$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{help}\:! \\ $$
Answered by MJS_new last updated on 19/Oct/20
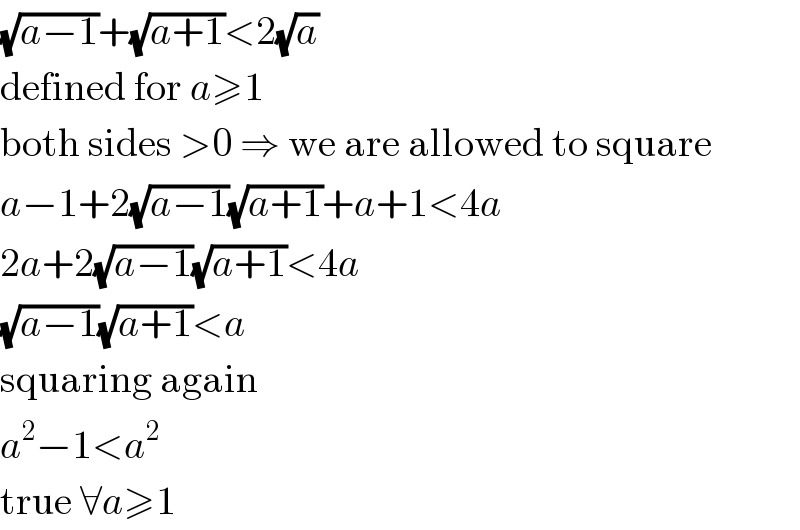
$$\sqrt{{a}−\mathrm{1}}+\sqrt{{a}+\mathrm{1}}<\mathrm{2}\sqrt{{a}} \\ $$$$\mathrm{defined}\:\mathrm{for}\:{a}\geqslant\mathrm{1} \\ $$$$\mathrm{both}\:\mathrm{sides}\:>\mathrm{0}\:\Rightarrow\:\mathrm{we}\:\mathrm{are}\:\mathrm{allowed}\:\mathrm{to}\:\mathrm{square} \\ $$$${a}−\mathrm{1}+\mathrm{2}\sqrt{{a}−\mathrm{1}}\sqrt{{a}+\mathrm{1}}+{a}+\mathrm{1}<\mathrm{4}{a} \\ $$$$\mathrm{2}{a}+\mathrm{2}\sqrt{{a}−\mathrm{1}}\sqrt{{a}+\mathrm{1}}<\mathrm{4}{a} \\ $$$$\sqrt{{a}−\mathrm{1}}\sqrt{{a}+\mathrm{1}}<{a} \\ $$$$\mathrm{squaring}\:\mathrm{again} \\ $$$${a}^{\mathrm{2}} −\mathrm{1}<{a}^{\mathrm{2}} \\ $$$$\mathrm{true}\:\forall{a}\geqslant\mathrm{1} \\ $$
Commented by greg_ed last updated on 20/Oct/20

$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{help}\:! \\ $$
Answered by 1549442205PVT last updated on 20/Oct/20
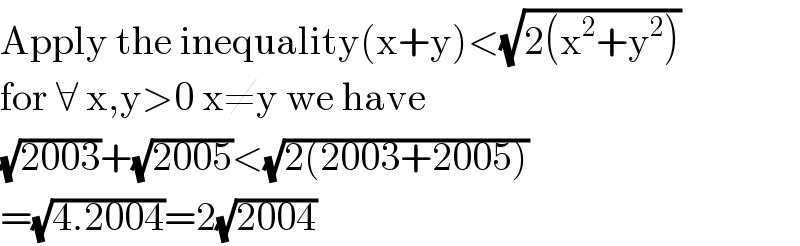
$$\mathrm{Apply}\:\mathrm{the}\:\mathrm{inequality}\left(\mathrm{x}+\mathrm{y}\right)<\sqrt{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}\: \\ $$$$\mathrm{for}\:\forall\:\mathrm{x},\mathrm{y}>\mathrm{0}\:\mathrm{x}\neq\mathrm{y}\:\mathrm{we}\:\mathrm{have} \\ $$$$\sqrt{\mathrm{2003}}+\sqrt{\mathrm{2005}}<\sqrt{\mathrm{2}\left(\mathrm{2003}+\mathrm{2005}\right)} \\ $$$$=\sqrt{\mathrm{4}.\mathrm{2004}}=\mathrm{2}\sqrt{\mathrm{2004}} \\ $$
Commented by greg_ed last updated on 20/Oct/20

$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{help}\:! \\ $$
Commented by 1549442205PVT last updated on 25/Oct/20

$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome} \\ $$
