Question Number 42366 by Joel578 last updated on 24/Aug/18
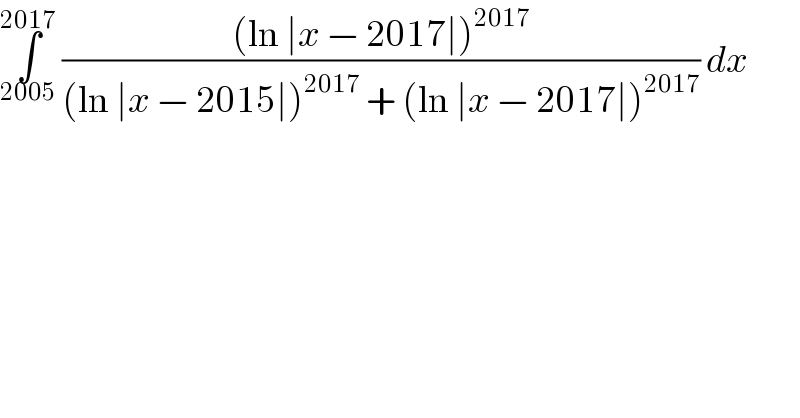
$$\underset{\mathrm{2005}} {\overset{\mathrm{2017}} {\int}}\:\frac{\left(\mathrm{ln}\:\mid{x}\:−\:\mathrm{2017}\mid\right)^{\mathrm{2017}} }{\left(\mathrm{ln}\:\mid{x}\:−\:\mathrm{2015}\mid\right)^{\mathrm{2017}} \:+\:\left(\mathrm{ln}\:\mid{x}\:−\:\mathrm{2017}\mid\right)^{\mathrm{2017}} }\:{dx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Aug/18
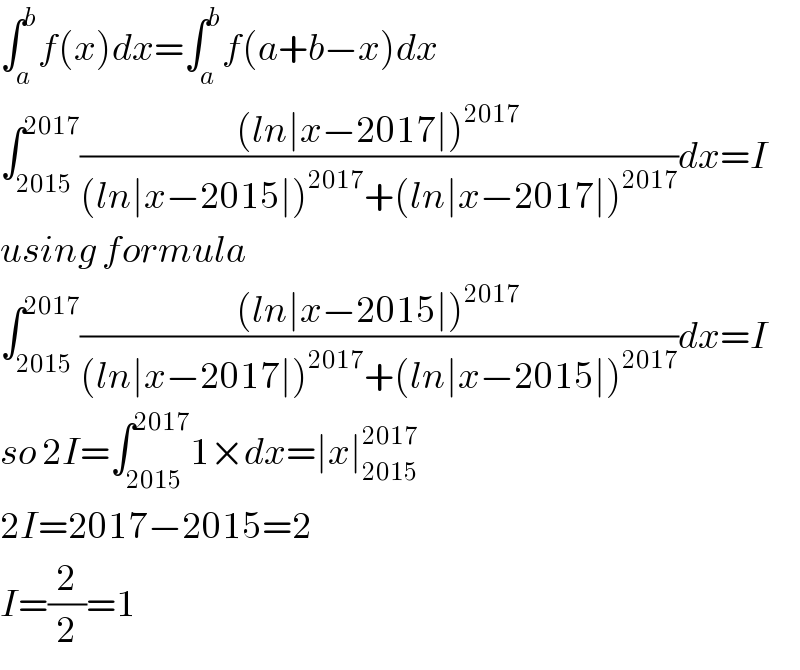
$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx} \\ $$$$\int_{\mathrm{2015}} ^{\mathrm{2017}} \frac{\left({ln}\mid{x}−\mathrm{2017}\mid\right)^{\mathrm{2017}} }{\left({ln}\mid{x}−\mathrm{2015}\mid\right)^{\mathrm{2017}} +\left({ln}\mid{x}−\mathrm{2017}\mid\right)^{\mathrm{2017}} }{dx}={I} \\ $$$${using}\:{formula} \\ $$$$\int_{\mathrm{2015}} ^{\mathrm{2017}} \frac{\left({ln}\mid{x}−\mathrm{2015}\mid\right)^{\mathrm{2017}} }{\left({ln}\mid{x}−\mathrm{2017}\mid\right)^{\mathrm{2017}} +\left({ln}\mid{x}−\mathrm{2015}\mid\right)^{\mathrm{2017}} }{dx}={I} \\ $$$${so}\:\mathrm{2}{I}=\int_{\mathrm{2015}} ^{\mathrm{2017}} \mathrm{1}×{dx}=\mid{x}\mid_{\mathrm{2015}} ^{\mathrm{2017}} \\ $$$$\mathrm{2}{I}=\mathrm{2017}−\mathrm{2015}=\mathrm{2} \\ $$$${I}=\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1} \\ $$
Commented by Joel578 last updated on 25/Aug/18
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Aug/18

$${its}\:{ok} \\ $$
