Question Number 89586 by Asif Hypothesis last updated on 18/Apr/20
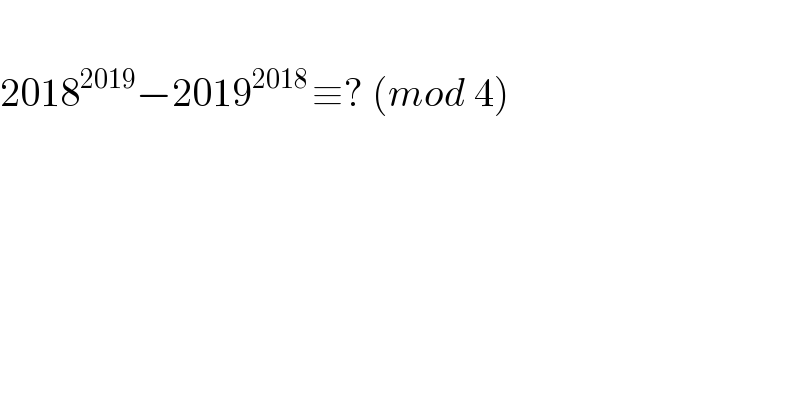
$$ \\ $$$$\mathrm{2018}^{\mathrm{2019}} −\mathrm{2019}^{\mathrm{2018}\:} \equiv?\:\left({mod}\:\mathrm{4}\right) \\ $$
Answered by Asif Hypothesis last updated on 18/Apr/20
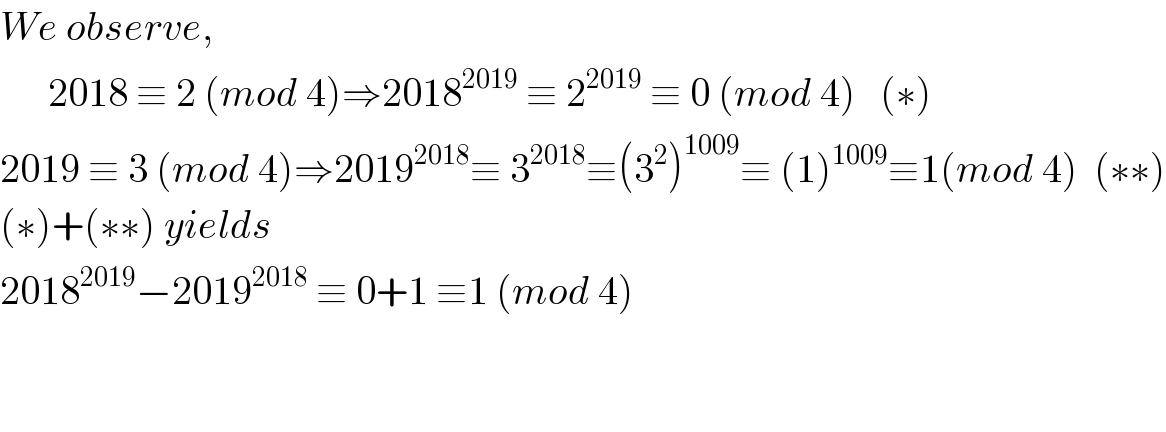
$${We}\:{observe}, \\ $$$$\:\:\:\:\:\:\mathrm{2018}\:\equiv\:\mathrm{2}\:\left({mod}\:\mathrm{4}\right)\Rightarrow\mathrm{2018}^{\mathrm{2019}} \:\equiv\:\mathrm{2}^{\mathrm{2019}} \:\equiv\:\mathrm{0}\:\left({mod}\:\mathrm{4}\right)\:\:\:\left(\ast\right) \\ $$$$\mathrm{2019}\:\equiv\:\mathrm{3}\:\left({mod}\:\mathrm{4}\right)\Rightarrow\mathrm{2019}^{\mathrm{2018}} \equiv\:\mathrm{3}^{\mathrm{2018}} \equiv\left(\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{1009}} \equiv\:\left(\mathrm{1}\right)^{\mathrm{1009}} \equiv\mathrm{1}\left({mod}\:\mathrm{4}\right)\:\:\left(\ast\ast\right) \\ $$$$\left(\ast\right)+\left(\ast\ast\right)\:{yields} \\ $$$$\mathrm{2018}^{\mathrm{2019}} −\mathrm{2019}^{\mathrm{2018}} \:\equiv\:\mathrm{0}+\mathrm{1}\:\equiv\mathrm{1}\:\left({mod}\:\mathrm{4}\right) \\ $$$$ \\ $$$$ \\ $$
