Question Number 130970 by naka3546 last updated on 31/Jan/21
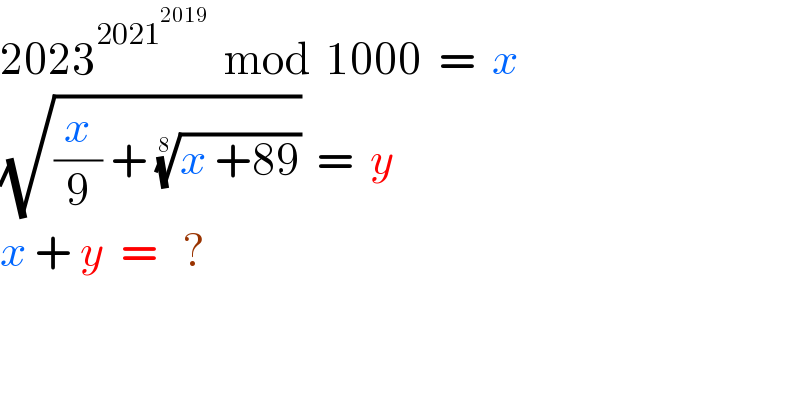
$$\mathrm{2023}^{\mathrm{2021}^{\mathrm{2019}} } \:\:\mathrm{mod}\:\:\mathrm{1000}\:\:=\:\:{x} \\ $$$$\sqrt{\frac{{x}}{\mathrm{9}}\:+\:\sqrt[{\mathrm{8}}]{{x}\:+\mathrm{89}}}\:\:=\:\:{y} \\ $$$${x}\:+\:{y}\:\:=\:\:\:? \\ $$
Commented by AlagaIbile last updated on 31/Jan/21

$$\:{Since}\:\boldsymbol{{gcd}}\left(\mathrm{2023},\mathrm{1000}\right)=\mathrm{1}. \\ $$$$\:\lambda\left(\mathrm{1000}\right)=\:\mathrm{100}\:,\:\lambda\left(\mathrm{100}\right)=\:\mathrm{20}.\:\lambda\left(\centerdot\right)\:{denote} \\ $$$$\:{Carmicheal}\:{Lambda}\:{Function} \\ $$$$\:\mathrm{2023}^{\mathrm{2021}^{\mathrm{2019}\:\:{mod}\:\mathrm{20}} \:{mod}\:\mathrm{100}} \:{mod}\:\mathrm{1000} \\ $$$$\:\equiv\:\mathrm{23}^{\mathrm{21}^{\mathrm{19}} \:{mod}\:\mathrm{100}} {mod}\:\mathrm{1000} \\ $$$$\:\equiv\:\mathrm{23}^{\mathrm{81}} \:\:\:{mod}\:\mathrm{1000} \\ $$$$\:\equiv\:\left(\mathrm{167}\right)^{\mathrm{27}} \:\equiv\:\left(\mathrm{463}\right)^{\mathrm{9}} \:\equiv\:\left(\mathrm{847}\right)^{\mathrm{3}} \:{mod}\:\mathrm{1000} \\ $$$$\:\boldsymbol{{x}}\:\equiv\:\mathrm{423}\:\:{mod}\:\mathrm{1000} \\ $$$$\:\therefore\:\boldsymbol{{y}}\:=\sqrt{\frac{\mathrm{423}}{\mathrm{9}}\:+\:\sqrt[{\mathrm{8}}]{\mathrm{423}+\mathrm{89}}}\:=\:\sqrt{\mathrm{47}\:+\:\sqrt[{\mathrm{8}}]{\mathrm{512}}} \\ $$$$\:\boldsymbol{{x}}\:+\:\boldsymbol{{y}}\:=\:\mathrm{423}\:+\:\sqrt{\mathrm{47}\:+\:\mathrm{2}\sqrt[{\mathrm{8}}]{\mathrm{2}}} \\ $$$$\:\boldsymbol{{Observation}}:\:{To}\:{make}\:\boldsymbol{{y}}\:{an}\:{integer}\:{the}\:{question}\:{should}\:{ask}\:{for} \\ $$$$\:\boldsymbol{{y}}\:=\:\sqrt{\frac{\boldsymbol{{x}}}{\mathrm{9}}\:+\:\sqrt[{\mathrm{9}}]{\boldsymbol{{x}}\:+\:\mathrm{89}}}\:=\:\mathrm{7} \\ $$$$\therefore\:\boldsymbol{{x}}\:+\:\boldsymbol{{y}}\:=\:\mathrm{423}\:+\:\mathrm{7}\:=\:\mathrm{450} \\ $$
Commented by naka3546 last updated on 31/Jan/21
$${Thank}\:{you},\:{sir}. \\ $$
