Menu Close

2207-1-2207-1-2207-1-2207-1-2207-1-8-

Tinku Tara 0 Comments
Pin




Question Number 128264 by bobhans last updated on 06/Jan/21
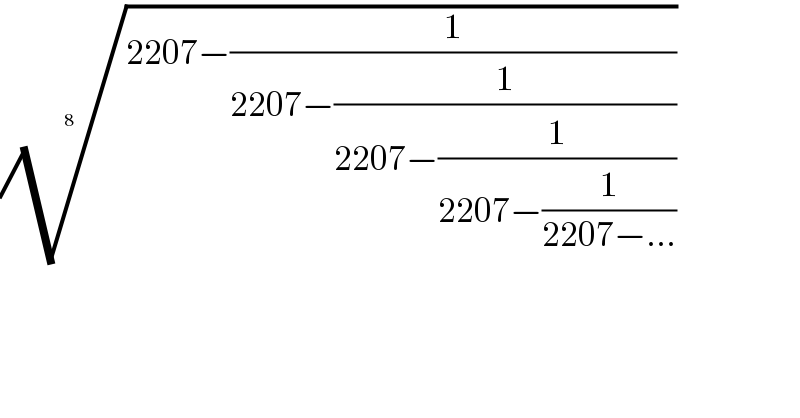
((2207−(1/(2207−(1/(2207−(1/(2207−(1/(2207−...))))))))))^(1/(8 ))
$$\sqrt[{\mathrm{8}\:\:\:\:}]{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−…}}}}} \\ $$
Commented by MJS_new last updated on 06/Jan/21
((3+(√5))/2)
$$\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by bobhans last updated on 06/Jan/21
waw....how?
$${waw}….{how}? \\ $$
Commented by liberty last updated on 06/Jan/21
((2207−(1/(2207−(1/(2207−(1/(2207−...))))))))^(1/(8 )) = ((a+b(√c))/d) ; a,b,c,d ∈ Z let x =((2207−(1/x^8 )))^(1/(8 )) ⇒x^8 =2207−(1/x^8 ) ⇒x^(16) −2207x^8 +1 = (x^8 +px^4 +1)(x^8 −px^4 +1) we find p^2 =2209 →p=47 ⇒x^(16) −2207x^8 +1=(x^8 +47x^4 +1)(x^8 −47x^4 +1) now x^8 +47x^2 +1=(x^4 +qx^2 +1)(x^4 −qx^2 +1) we get q= 7 x^8 +47x^2 +1=(x^4 +7x^2 +1) then x^(16) −2207x^8 +1=(x^8 +47x^4 +1)(x^4 +7x+1)(x^2 +3x+1)(x^2 −3x+1) x must be a root x^2 −3x+1=0 ⇒ x = ((3+(√5))/2) > 2 or x=((3−(√5))/2) < 2 x = ((2207−(1/(2207−x^8 ))))^(1/8) > ((2207−(1/(2207))))^(1/(8 )) >((256))^(1/(8 )) = 2 so the solution is x=((3+(√5))/2)
$$\sqrt[{\mathrm{8}\:}]{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−…}}}}\:=\:\frac{{a}+{b}\sqrt{{c}}}{{d}}\:;\:{a},{b},{c},{d}\:\in\:\mathbb{Z} \\ $$$$\mathrm{let}\:{x}\:=\sqrt[{\mathrm{8}\:}]{\mathrm{2207}−\frac{\mathrm{1}}{{x}^{\mathrm{8}} }}\:\Rightarrow{x}^{\mathrm{8}} =\mathrm{2207}−\frac{\mathrm{1}}{{x}^{\mathrm{8}} } \\ $$$$\Rightarrow{x}^{\mathrm{16}} −\mathrm{2207}{x}^{\mathrm{8}} +\mathrm{1}\:=\:\left({x}^{\mathrm{8}} +{px}^{\mathrm{4}} +\mathrm{1}\right)\left({x}^{\mathrm{8}} −{px}^{\mathrm{4}} +\mathrm{1}\right) \\ $$$$\:{we}\:{find}\:{p}^{\mathrm{2}} =\mathrm{2209}\:\rightarrow\mathrm{p}=\mathrm{47} \\ $$$$\Rightarrow{x}^{\mathrm{16}} −\mathrm{2207}{x}^{\mathrm{8}} +\mathrm{1}=\left({x}^{\mathrm{8}} +\mathrm{47}{x}^{\mathrm{4}} +\mathrm{1}\right)\left({x}^{\mathrm{8}} −\mathrm{47}{x}^{\mathrm{4}} +\mathrm{1}\right) \\ $$$${now}\:{x}^{\mathrm{8}} +\mathrm{47}{x}^{\mathrm{2}} +\mathrm{1}=\left({x}^{\mathrm{4}} +{qx}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} −{qx}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${we}\:{get}\:{q}=\:\mathrm{7} \\ $$$${x}^{\mathrm{8}} +\mathrm{47}{x}^{\mathrm{2}} +\mathrm{1}=\left({x}^{\mathrm{4}} +\mathrm{7}{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${then}\:{x}^{\mathrm{16}} −\mathrm{2207}{x}^{\mathrm{8}} +\mathrm{1}=\left({x}^{\mathrm{8}} +\mathrm{47}{x}^{\mathrm{4}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} +\mathrm{7}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}\right) \\ $$$${x}\:{must}\:{be}\:{a}\:{root}\:{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{x}\:=\:\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:>\:\mathrm{2}\:{or}\:{x}=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:<\:\mathrm{2} \\ $$$${x}\:=\:\sqrt[{\mathrm{8}}]{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−{x}^{\mathrm{8}} }}\:>\:\sqrt[{\mathrm{8}\:}]{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}}}\:>\sqrt[{\mathrm{8}\:}]{\mathrm{256}}\:=\:\mathrm{2} \\ $$$${so}\:{the}\:{solution}\:{is}\:{x}=\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Answered by MJS_new last updated on 06/Jan/21
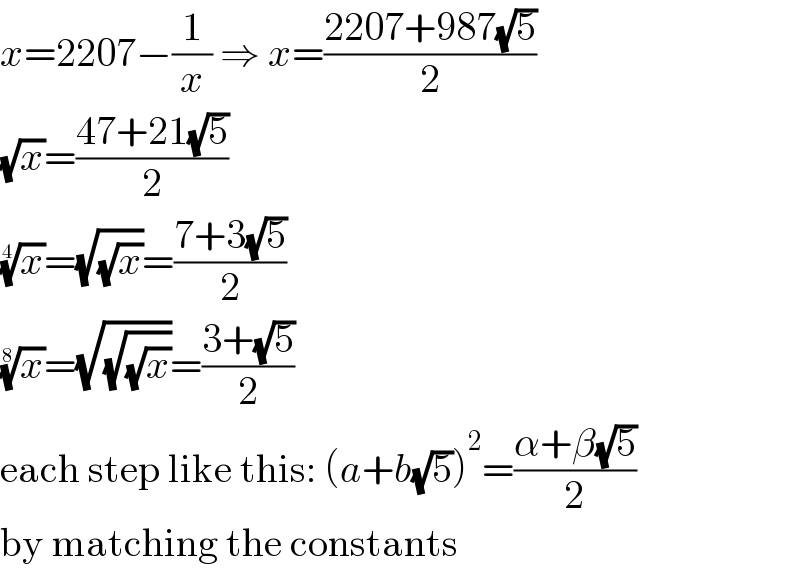
x=2207−(1/x) ⇒ x=((2207+987(√5))/2) (√x)=((47+21(√5))/2) (x)^(1/4) =(√(√x))=((7+3(√5))/2) (x)^(1/8) =(√(√(√x)))=((3+(√5))/2) each step like this: (a+b(√5))^2 =((α+β(√5))/2) by matching the constants
$${x}=\mathrm{2207}−\frac{\mathrm{1}}{{x}}\:\Rightarrow\:{x}=\frac{\mathrm{2207}+\mathrm{987}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\sqrt{{x}}=\frac{\mathrm{47}+\mathrm{21}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\sqrt[{\mathrm{4}}]{{x}}=\sqrt{\sqrt{{x}}}=\frac{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\sqrt[{\mathrm{8}}]{{x}}=\sqrt{\sqrt{\sqrt{{x}}}}=\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{each}\:\mathrm{step}\:\mathrm{like}\:\mathrm{this}:\:\left({a}+{b}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} =\frac{\alpha+\beta\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{by}\:\mathrm{matching}\:\mathrm{the}\:\mathrm{constants} \\ $$
Commented by mr W last updated on 06/Jan/21
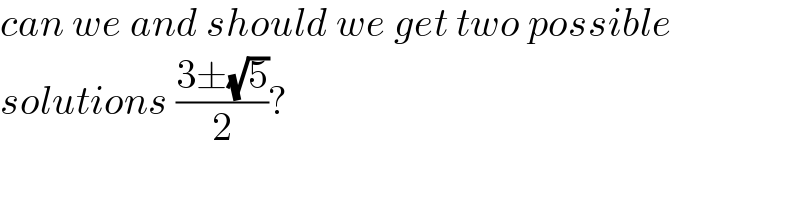
can we and should we get two possible solutions ((3±(√5))/2)?
$${can}\:{we}\:{and}\:{should}\:{we}\:{get}\:{two}\:{possible} \\ $$$${solutions}\:\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}? \\ $$
Commented by MJS_new last updated on 06/Jan/21
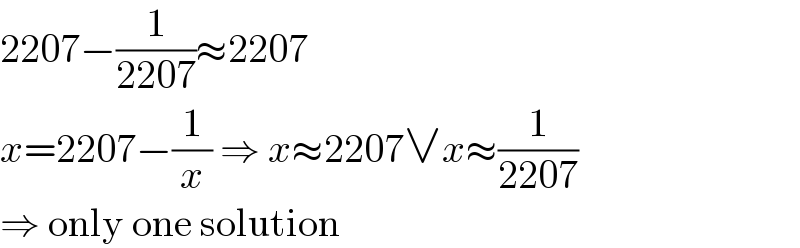
2207−(1/(2207))≈2207 x=2207−(1/x) ⇒ x≈2207∨x≈(1/(2207)) ⇒ only one solution
$$\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}}\approx\mathrm{2207} \\ $$$${x}=\mathrm{2207}−\frac{\mathrm{1}}{{x}}\:\Rightarrow\:{x}\approx\mathrm{2207}\vee{x}\approx\frac{\mathrm{1}}{\mathrm{2207}} \\ $$$$\Rightarrow\:\mathrm{only}\:\mathrm{one}\:\mathrm{solution} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *