Question Number 149423 by mathdanisur last updated on 05/Aug/21
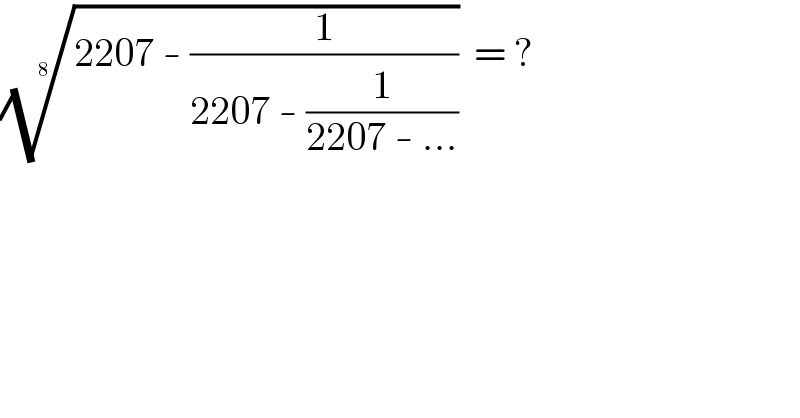
$$\sqrt[{\mathrm{8}}]{\mathrm{2207}\:-\:\frac{\mathrm{1}}{\mathrm{2207}\:-\:\frac{\mathrm{1}}{\mathrm{2207}\:-\:…}}}\:\:=\:? \\ $$
Answered by dumitrel last updated on 05/Aug/21
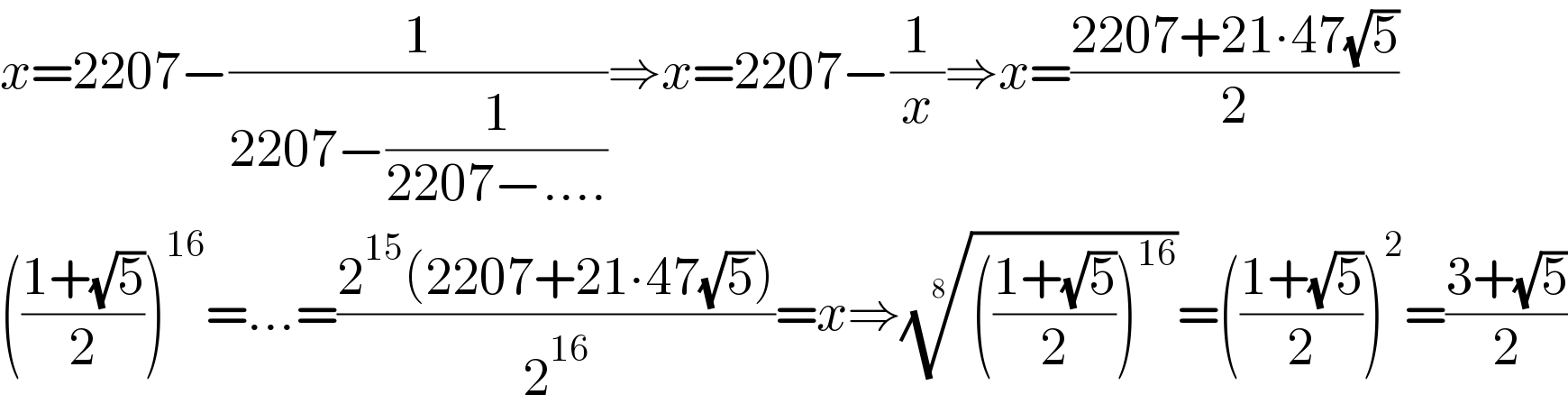
$${x}=\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−….}}\Rightarrow{x}=\mathrm{2207}−\frac{\mathrm{1}}{{x}}\Rightarrow{x}=\frac{\mathrm{2207}+\mathrm{21}\centerdot\mathrm{47}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{16}} =…=\frac{\mathrm{2}^{\mathrm{15}} \left(\mathrm{2207}+\mathrm{21}\centerdot\mathrm{47}\sqrt{\mathrm{5}}\right)}{\mathrm{2}^{\mathrm{16}} }={x}\Rightarrow\sqrt[{\mathrm{8}}]{\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{16}} }=\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 05/Aug/21

$${Thank}\:{You}\:{Ser},\:{Cool} \\ $$
