Question Number 31677 by gyugfeet last updated on 12/Mar/18
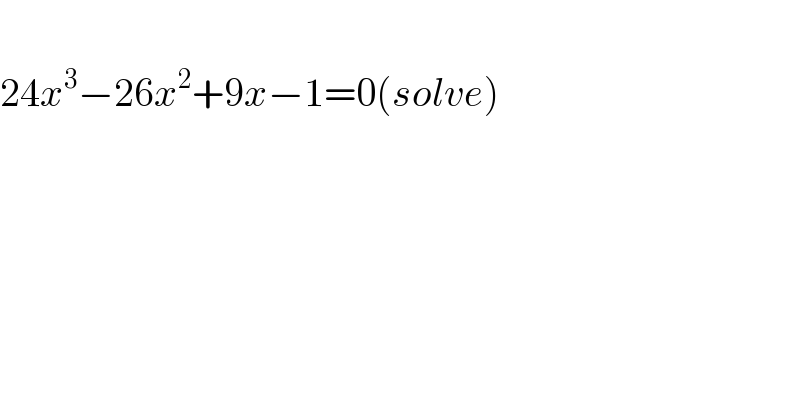
$$ \\ $$$$\mathrm{24}{x}^{\mathrm{3}} −\mathrm{26}{x}^{\mathrm{2}} +\mathrm{9}{x}−\mathrm{1}=\mathrm{0}\left({solve}\right) \\ $$
Answered by Joel578 last updated on 12/Mar/18
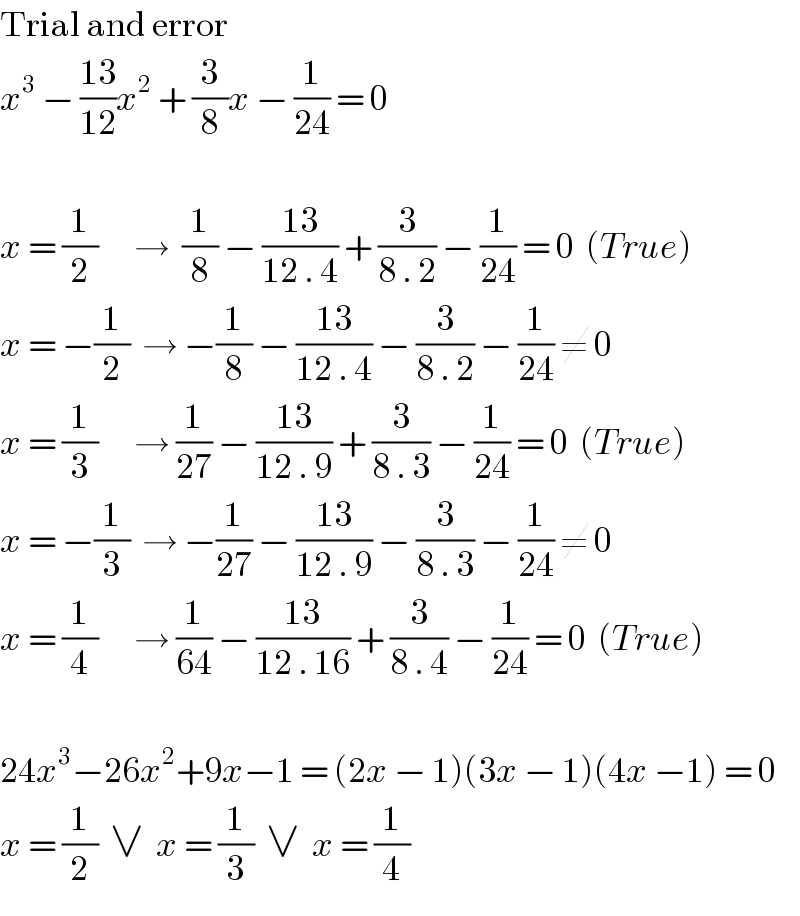
$$\mathrm{Trial}\:\mathrm{and}\:\mathrm{error} \\ $$$${x}^{\mathrm{3}} \:−\:\frac{\mathrm{13}}{\mathrm{12}}{x}^{\mathrm{2}} \:+\:\frac{\mathrm{3}}{\mathrm{8}}{x}\:−\:\frac{\mathrm{1}}{\mathrm{24}}\:=\:\mathrm{0} \\ $$$$ \\ $$$${x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\rightarrow\:\:\frac{\mathrm{1}}{\mathrm{8}}\:−\:\frac{\mathrm{13}}{\mathrm{12}\:.\:\mathrm{4}}\:+\:\frac{\mathrm{3}}{\mathrm{8}\:.\:\mathrm{2}}\:−\:\frac{\mathrm{1}}{\mathrm{24}}\:=\:\mathrm{0}\:\:\left({True}\right) \\ $$$${x}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\:\:\rightarrow\:−\frac{\mathrm{1}}{\mathrm{8}}\:−\:\frac{\mathrm{13}}{\mathrm{12}\:.\:\mathrm{4}}\:−\:\frac{\mathrm{3}}{\mathrm{8}\:.\:\mathrm{2}}\:−\:\frac{\mathrm{1}}{\mathrm{24}}\:\neq\:\mathrm{0}\:\:\: \\ $$$${x}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\:\:\rightarrow\:\frac{\mathrm{1}}{\mathrm{27}}\:−\:\frac{\mathrm{13}}{\mathrm{12}\:.\:\mathrm{9}}\:+\:\frac{\mathrm{3}}{\mathrm{8}\:.\:\mathrm{3}}\:−\:\frac{\mathrm{1}}{\mathrm{24}}\:=\:\mathrm{0}\:\:\left({True}\right) \\ $$$${x}\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\:\:\rightarrow\:−\frac{\mathrm{1}}{\mathrm{27}}\:−\:\frac{\mathrm{13}}{\mathrm{12}\:.\:\mathrm{9}}\:−\:\frac{\mathrm{3}}{\mathrm{8}\:.\:\mathrm{3}}\:−\:\frac{\mathrm{1}}{\mathrm{24}}\:\neq\:\mathrm{0} \\ $$$${x}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\:\rightarrow\:\frac{\mathrm{1}}{\mathrm{64}}\:−\:\frac{\mathrm{13}}{\mathrm{12}\:.\:\mathrm{16}}\:+\:\frac{\mathrm{3}}{\mathrm{8}\:.\:\mathrm{4}}\:−\:\frac{\mathrm{1}}{\mathrm{24}}\:=\:\mathrm{0}\:\:\left({True}\right) \\ $$$$ \\ $$$$\mathrm{24}{x}^{\mathrm{3}} −\mathrm{26}{x}^{\mathrm{2}} +\mathrm{9}{x}−\mathrm{1}\:=\:\left(\mathrm{2}{x}\:−\:\mathrm{1}\right)\left(\mathrm{3}{x}\:−\:\mathrm{1}\right)\left(\mathrm{4}{x}\:−\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$${x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\vee\:\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\:\vee\:\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by MJS last updated on 12/Mar/18
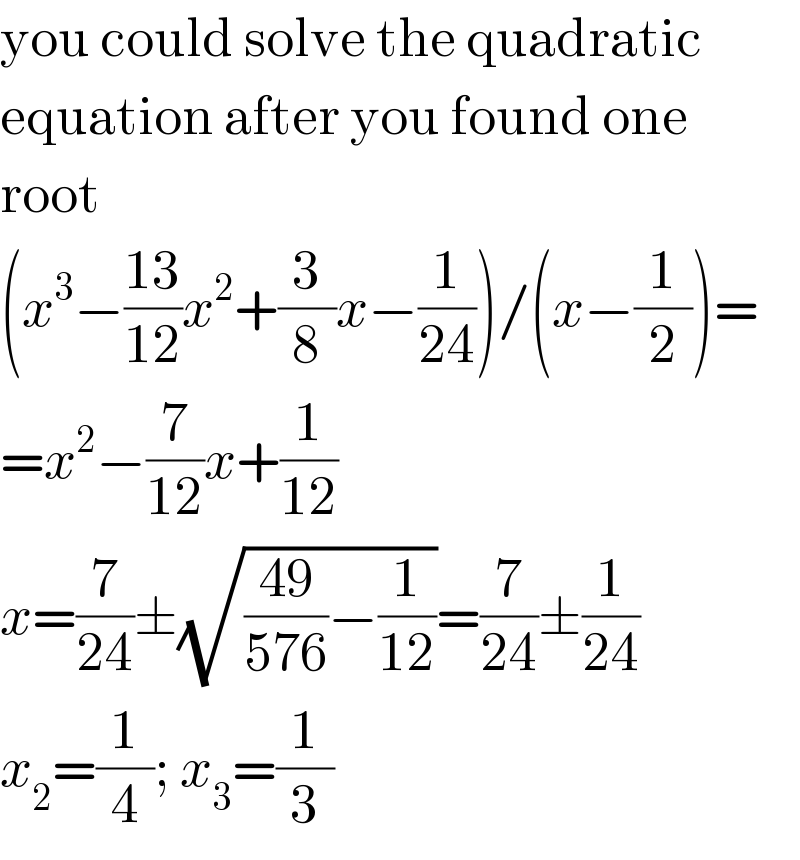
$$\mathrm{you}\:\mathrm{could}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{quadratic} \\ $$$$\mathrm{equation}\:\mathrm{after}\:\mathrm{you}\:\mathrm{found}\:\mathrm{one} \\ $$$$\mathrm{root} \\ $$$$\left({x}^{\mathrm{3}} −\frac{\mathrm{13}}{\mathrm{12}}{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{8}}{x}−\frac{\mathrm{1}}{\mathrm{24}}\right)/\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)= \\ $$$$={x}^{\mathrm{2}} −\frac{\mathrm{7}}{\mathrm{12}}{x}+\frac{\mathrm{1}}{\mathrm{12}} \\ $$$${x}=\frac{\mathrm{7}}{\mathrm{24}}\pm\sqrt{\frac{\mathrm{49}}{\mathrm{576}}−\frac{\mathrm{1}}{\mathrm{12}}}=\frac{\mathrm{7}}{\mathrm{24}}\pm\frac{\mathrm{1}}{\mathrm{24}} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}};\:{x}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by Joel578 last updated on 12/Mar/18
$${thanks}\:{for}\:{suggestion} \\ $$
