Question Number 31846 by momo last updated on 15/Mar/18
![25[(x−2)^2 +(y−3)^2 ]=(3x−4y+7)^2 is the equation of parabola.Find length of latus rectum](https://www.tinkutara.com/question/Q31846.png)
$$\mathrm{25}\left[\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} \right]=\left(\mathrm{3}{x}−\mathrm{4}{y}+\mathrm{7}\right)^{\mathrm{2}} \\ $$$${is}\:{the}\:{equation}\:{of}\:{parabola}.{Find} \\ $$$${length}\:{of}\:{latus}\:{rectum} \\ $$
Commented by momo last updated on 16/Mar/18

$${how} \\ $$
Commented by momo last updated on 16/Mar/18
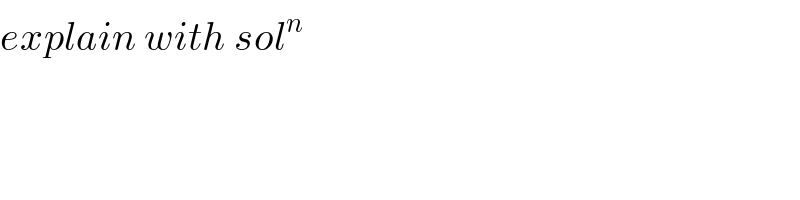
$${explain}\:{with}\:{sol}^{{n}} \\ $$
Answered by Tinkutara last updated on 16/Mar/18
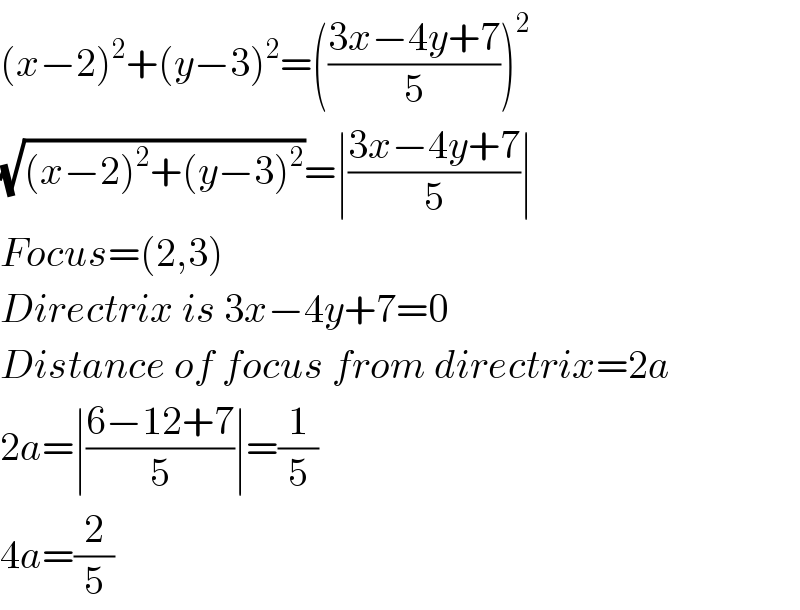
$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} =\left(\frac{\mathrm{3}{x}−\mathrm{4}{y}+\mathrm{7}}{\mathrm{5}}\right)^{\mathrm{2}} \\ $$$$\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} }=\mid\frac{\mathrm{3}{x}−\mathrm{4}{y}+\mathrm{7}}{\mathrm{5}}\mid \\ $$$${Focus}=\left(\mathrm{2},\mathrm{3}\right) \\ $$$${Directrix}\:{is}\:\mathrm{3}{x}−\mathrm{4}{y}+\mathrm{7}=\mathrm{0} \\ $$$${Distance}\:{of}\:{focus}\:{from}\:{directrix}=\mathrm{2}{a} \\ $$$$\mathrm{2}{a}=\mid\frac{\mathrm{6}−\mathrm{12}+\mathrm{7}}{\mathrm{5}}\mid=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\mathrm{4}{a}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$
Commented by momo last updated on 16/Mar/18

$${thanks}\:{sir} \\ $$
