Menu Close

26-R-1-37-1-R-2-3-2-R-3-5-Find-R-1-R-2-and-R-3-

Tinku Tara 0 Comments
Pin




Question Number 90200 by Ar Brandon last updated on 21/Apr/20
26≡R_1 [37] 1 ≡R_2 [3] 2≡R_3 [5] Find R_1 , R_2 and R_3
$$\mathrm{26}\equiv\mathrm{R}_{\mathrm{1}} \left[\mathrm{37}\right] \\ $$$$\mathrm{1}\:\:\equiv\mathrm{R}_{\mathrm{2}} \left[\mathrm{3}\right] \\ $$$$\mathrm{2}\equiv\mathrm{R}_{\mathrm{3}} \left[\mathrm{5}\right] \\ $$$$\mathrm{Find}\:\mathrm{R}_{\mathrm{1}} ,\:\mathrm{R}_{\mathrm{2}} \mathrm{and}\:\mathrm{R}_{\mathrm{3}} \\ $$
Commented by Rio Michael last updated on 22/Apr/20
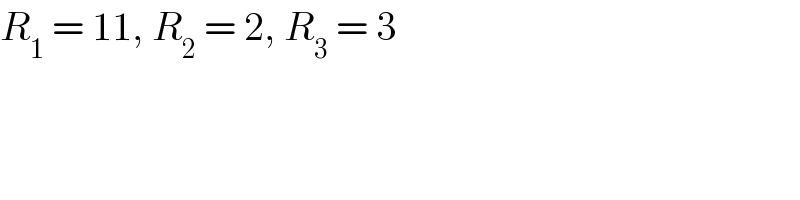
R_1 = 11, R_2 = 2, R_3 = 3
$${R}_{\mathrm{1}} \:=\:\mathrm{11},\:{R}_{\mathrm{2}} \:=\:\mathrm{2},\:{R}_{\mathrm{3}} \:=\:\mathrm{3} \\ $$
Commented by Ar Brandon last updated on 22/Apr/20
Thanks, but how?
$$\mathrm{Thanks},\:\mathrm{but}\:\mathrm{how}? \\ $$
Commented by Rio Michael last updated on 22/Apr/20
if your question is actually 26 ≡ R_1 (mod 37) ⇒ R_1 is the reminder when 26 is divided by 37 which rightly is 11. or you can say by definition a ≡ b (mod n) ⇔ n ∣(a−b) ⇒ a−b = nk , k∈Z ⇒ 26 ≡ R_1 (mod 37) ⇒ 26 = 37 k + R k =0 R_1 = 26 k = 1 ⇒ R_1 = −11 k = −1⇒ R_1 = 63 these are just the elements of the set of least residue mod 37.
$$\mathrm{if}\:\mathrm{your}\:\mathrm{question}\:\mathrm{is}\:\mathrm{actually} \\ $$$$\:\mathrm{26}\:\equiv\:{R}_{\mathrm{1}} \:\left(\mathrm{mod}\:\mathrm{37}\right)\:\Rightarrow\:\mathrm{R}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{reminder}\:\mathrm{when}\:\mathrm{26}\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{37} \\ $$$$\mathrm{which}\:\mathrm{rightly}\:\mathrm{is}\:\mathrm{11}. \\ $$$$\mathrm{or}\:\mathrm{you}\:\mathrm{can}\:\mathrm{say} \\ $$$$\:\:\:\mathrm{by}\:\mathrm{definition}\:{a}\:\equiv\:{b}\:\left(\mathrm{mod}\:{n}\right)\:\Leftrightarrow\:{n}\:\mid\left({a}−{b}\right)\:\Rightarrow\:{a}−{b}\:=\:{nk}\:,\:{k}\in\mathbb{Z} \\ $$$$\Rightarrow\:\mathrm{26}\:\equiv\:{R}_{\mathrm{1}} \:\left(\mathrm{mod}\:\mathrm{37}\right)\:\Rightarrow\:\:\mathrm{26}\:=\:\mathrm{37}\:{k}\:+\:{R} \\ $$$${k}\:=\mathrm{0}\:\:\mathrm{R}_{\mathrm{1}} \:=\:\mathrm{26} \\ $$$${k}\:=\:\mathrm{1}\:\Rightarrow\:{R}_{\mathrm{1}} \:=\:−\mathrm{11} \\ $$$${k}\:=\:−\mathrm{1}\Rightarrow\:{R}_{\mathrm{1}} \:=\:\mathrm{63} \\ $$$$\mathrm{these}\:\mathrm{are}\:\mathrm{just}\:\mathrm{the}\:\mathrm{elements}\:\mathrm{of}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{least}\:\mathrm{residue}\:\mathrm{mod}\:\mathrm{37}. \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 22/Apr/20
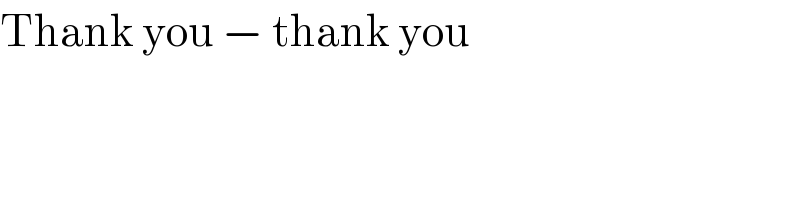
Thank you − thank you
$$\mathrm{Thank}\:\mathrm{you}\:−\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mr W last updated on 22/Apr/20
how can you say 26≡R_1 mod 37 ⇒R_1 =11? that means then 26=37k+11. this is wrong! clearly: R_1 =26 since 26≡26 mod 37 R_2 =1 R_3 =2
$${how}\:{can}\:{you}\:{say} \\ $$$$\mathrm{26}\equiv{R}_{\mathrm{1}} \:{mod}\:\mathrm{37}\:\Rightarrow{R}_{\mathrm{1}} =\mathrm{11}? \\ $$$${that}\:{means}\:{then}\:\mathrm{26}=\mathrm{37}{k}+\mathrm{11}. \\ $$$${this}\:{is}\:{wrong}! \\ $$$${clearly}: \\ $$$${R}_{\mathrm{1}} =\mathrm{26}\:{since}\:\mathrm{26}\equiv\mathrm{26}\:{mod}\:\mathrm{37} \\ $$$${R}_{\mathrm{2}} =\mathrm{1} \\ $$$${R}_{\mathrm{3}} =\mathrm{2} \\ $$
Commented by Ar Brandon last updated on 22/Apr/20
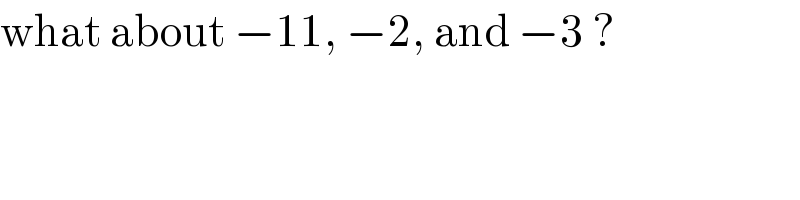
what about −11, −2, and −3 ?
$$\mathrm{what}\:\mathrm{about}\:−\mathrm{11},\:−\mathrm{2},\:\mathrm{and}\:−\mathrm{3}\:? \\ $$
Commented by mr W last updated on 22/Apr/20
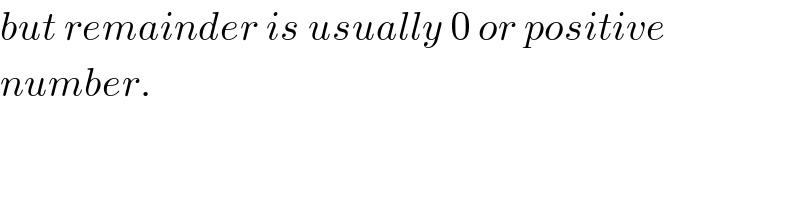
but remainder is usually 0 or positive number.
$${but}\:{remainder}\:{is}\:{usually}\:\mathrm{0}\:{or}\:{positive} \\ $$$${number}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *