Question Number 184434 by a.lgnaoui last updated on 06/Jan/23
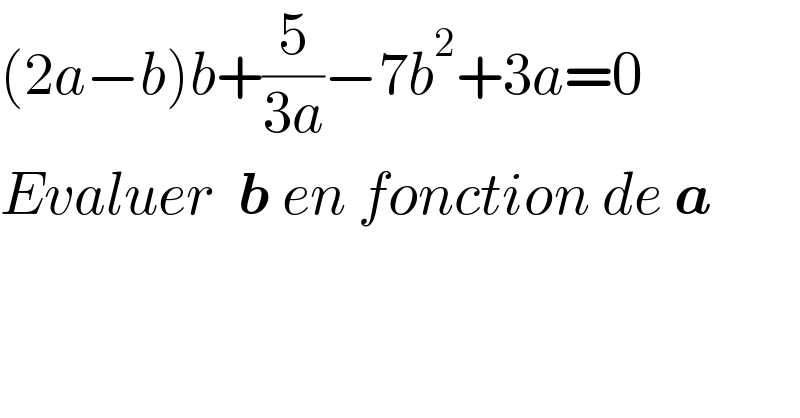
$$\left(\mathrm{2}{a}−{b}\right){b}+\frac{\mathrm{5}}{\mathrm{3}{a}}−\mathrm{7}{b}^{\mathrm{2}} +\mathrm{3}{a}=\mathrm{0} \\ $$$${Evaluer}\:\:\boldsymbol{{b}}\:{en}\:{fonction}\:{de}\:\boldsymbol{{a}} \\ $$
Answered by Frix last updated on 06/Jan/23
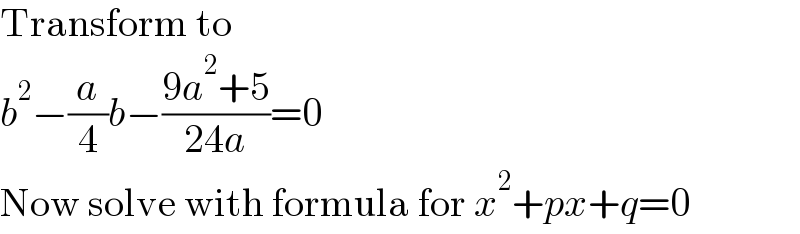
$$\mathrm{Transform}\:\mathrm{to} \\ $$$${b}^{\mathrm{2}} −\frac{{a}}{\mathrm{4}}{b}−\frac{\mathrm{9}{a}^{\mathrm{2}} +\mathrm{5}}{\mathrm{24}{a}}=\mathrm{0} \\ $$$$\mathrm{Now}\:\mathrm{solve}\:\mathrm{with}\:\mathrm{formula}\:\mathrm{for}\:{x}^{\mathrm{2}} +{px}+{q}=\mathrm{0} \\ $$
Commented by a.lgnaoui last updated on 06/Jan/23

$${thanks}\: \\ $$
Answered by a.lgnaoui last updated on 06/Jan/23
![6a^2 b−3ab^2 +5−21ab^2 +9a^2 =0 6a^2 b−24ab^2 +9a^2 +5=0 9a^2 +5−24a[b^2 −((ab)/4)]=0 9a^2 +5−24a[(b−(a/8))^2 −(a^2 /(64))]=0 9a^2 +5−24a(b−(a/8))^2 +((3a^3 )/8)=0 ((3a^3 )/8)+9a^2 +5=24a(b−(a/8))^2 b=(√(((a/9))^2 +((3a)/8)+(5/(24a)))) +(a/8)](https://www.tinkutara.com/question/Q184452.png)
$$\mathrm{6}{a}^{\mathrm{2}} {b}−\mathrm{3}{ab}^{\mathrm{2}} +\mathrm{5}−\mathrm{21}{ab}^{\mathrm{2}} +\mathrm{9}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{6}{a}^{\mathrm{2}} {b}−\mathrm{24}{ab}^{\mathrm{2}} +\mathrm{9}{a}^{\mathrm{2}} +\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{9}{a}^{\mathrm{2}} +\mathrm{5}−\mathrm{24}{a}\left[{b}^{\mathrm{2}} −\frac{{ab}}{\mathrm{4}}\right]=\mathrm{0} \\ $$$$\mathrm{9}{a}^{\mathrm{2}} +\mathrm{5}−\mathrm{24}{a}\left[\left({b}−\frac{{a}}{\mathrm{8}}\right)^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{64}}\right]=\mathrm{0} \\ $$$$\mathrm{9}{a}^{\mathrm{2}} +\mathrm{5}−\mathrm{24}{a}\left({b}−\frac{{a}}{\mathrm{8}}\right)^{\mathrm{2}} +\frac{\mathrm{3}{a}^{\mathrm{3}} }{\mathrm{8}}=\mathrm{0} \\ $$$$\frac{\mathrm{3}{a}^{\mathrm{3}} }{\mathrm{8}}+\mathrm{9}{a}^{\mathrm{2}} +\mathrm{5}=\mathrm{24}{a}\left({b}−\frac{{a}}{\mathrm{8}}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${b}=\sqrt{\left(\frac{{a}}{\mathrm{9}}\right)^{\mathrm{2}} +\frac{\mathrm{3}{a}}{\mathrm{8}}+\frac{\mathrm{5}}{\mathrm{24}{a}}}\:+\frac{{a}}{\mathrm{8}} \\ $$$$ \\ $$
