Question Number 40875 by Tawa1 last updated on 28/Jul/18
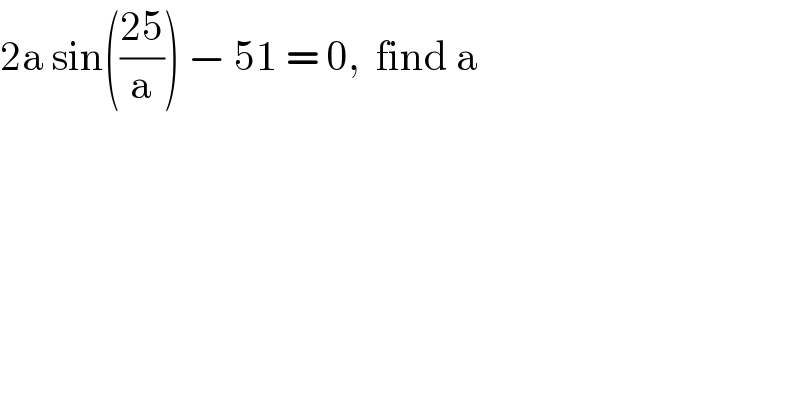
$$\mathrm{2a}\:\mathrm{sin}\left(\frac{\mathrm{25}}{\mathrm{a}}\right)\:−\:\mathrm{51}\:=\:\mathrm{0},\:\:\mathrm{find}\:\mathrm{a} \\ $$
Answered by MrW3 last updated on 29/Jul/18

$${let}'{s}\:{have}\:{a}\:{look}\:{at}\:{the}\:{function}\:{f}\left({x}\right)=\frac{\mathrm{sin}\:\left({x}\right)}{{x}}. \\ $$$${we}\:{know}\:{following}\:{about}\:{it}: \\ $$$${f}\left(−{x}\right)={f}\left({x}\right)\:\Rightarrow{symmetric} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({x}\right)=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{f}\left({x}\right)=\mathrm{0} \\ $$$${max}.\:{f}\left({x}\right)=\mathrm{1} \\ $$$${min}.\:{f}\left({x}\right)=−\mathrm{0}.\mathrm{2172} \\ $$$${i}.{e}.\:−\mathrm{0}.\mathrm{2172}\leqslant{f}\left({x}\right)<\mathrm{1} \\ $$$$ \\ $$$$\mathrm{2}{a}\:\mathrm{sin}\:\left(\frac{\mathrm{25}}{{a}}\right)=\mathrm{50}×\frac{\mathrm{sin}\:\left(\frac{\mathrm{25}}{{a}}\right)}{\left(\frac{\mathrm{25}}{{a}}\right)}=\mathrm{50}\:\frac{\mathrm{sin}\:\left({x}\right)}{{x}}=\mathrm{50}\:{f}\left({x}\right)\:{with}\:{x}=\frac{\mathrm{25}}{{a}} \\ $$$${since}\:{f}\left({x}\right)<\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{a}\:\mathrm{sin}\:\left(\frac{\mathrm{25}}{{a}}\right)=\mathrm{50}\:{f}\left({x}\right)<\mathrm{50} \\ $$$$\Rightarrow\mathrm{2}{a}\:\mathrm{sin}\:\left(\frac{\mathrm{25}}{{a}}\right)−\mathrm{51}<−\mathrm{1} \\ $$$${that}'{t}\:{to}\:{say}\:\mathrm{2}\boldsymbol{{a}}\:\boldsymbol{\mathrm{sin}}\:\left(\frac{\mathrm{25}}{\boldsymbol{{a}}}\right)−\mathrm{51}=\mathrm{0}\:{is}\:{not} \\ $$$${possible}. \\ $$$$ \\ $$$$\Rightarrow{there}\:{is}\:{no}\:{solution}\:{for}\:{a}\:{which} \\ $$$${fulfills}\:\mathrm{2}\boldsymbol{{a}}\:\boldsymbol{\mathrm{sin}}\:\left(\frac{\mathrm{25}}{\boldsymbol{{a}}}\right)−\mathrm{51}=\mathrm{0}. \\ $$
Commented by Tawa1 last updated on 29/Jul/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
