Question Number 20884 by tammi last updated on 06/Sep/17
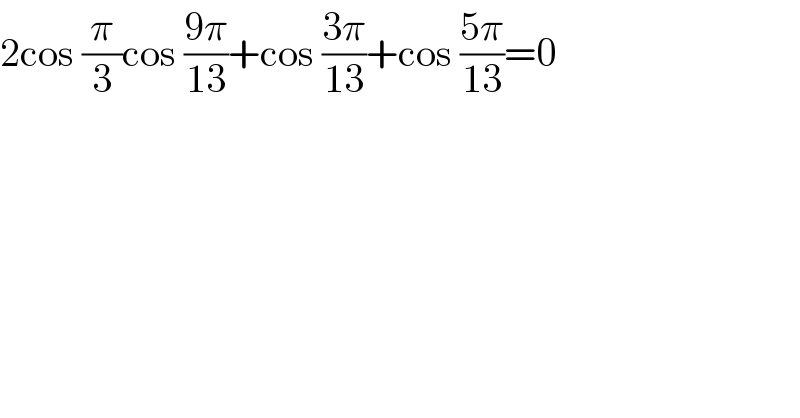
$$\mathrm{2cos}\:\frac{\pi}{\mathrm{3}}\mathrm{cos}\:\frac{\mathrm{9}\pi}{\mathrm{13}}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{13}}+\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{13}}=\mathrm{0} \\ $$
Answered by ajfour last updated on 06/Sep/17

$${must}\:{start}\:{with}\:\:\:\:\mathrm{2cos}\:\frac{\pi}{\mathrm{13}}…,\:{Then} \\ $$$$\:{L}.{H}.{S}.\:=\:\mathrm{cos}\:\left(\frac{\mathrm{10}\pi}{\mathrm{13}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{8}\pi}{\mathrm{13}}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{13}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{13}}\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{cos}\:\left(\pi−\frac{\mathrm{3}\pi}{\mathrm{13}}\right)+\mathrm{cos}\:\left(\pi−\frac{\mathrm{5}\pi}{\mathrm{13}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{13}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{13}}\right) \\ $$$$\:\:\:=−\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{13}}\right)−\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{13}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{13}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{13}}\right)\:=\:\mathrm{0}\:. \\ $$
