Question Number 82700 by jagoll last updated on 23/Feb/20
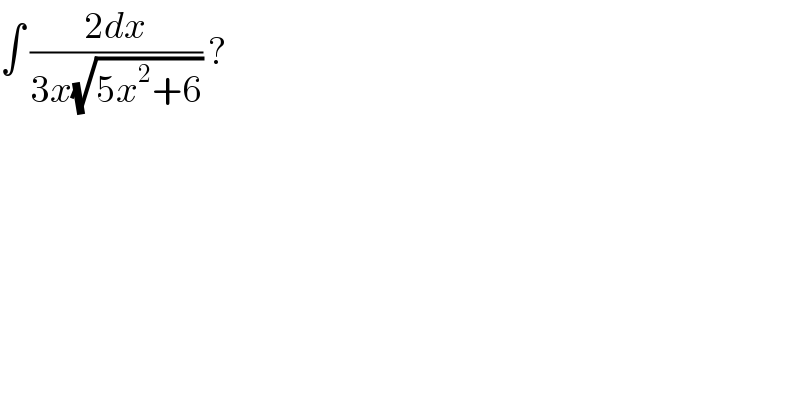
$$\int\:\frac{\mathrm{2}{dx}}{\mathrm{3}{x}\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{6}}}\:? \\ $$
Commented by john santu last updated on 23/Feb/20
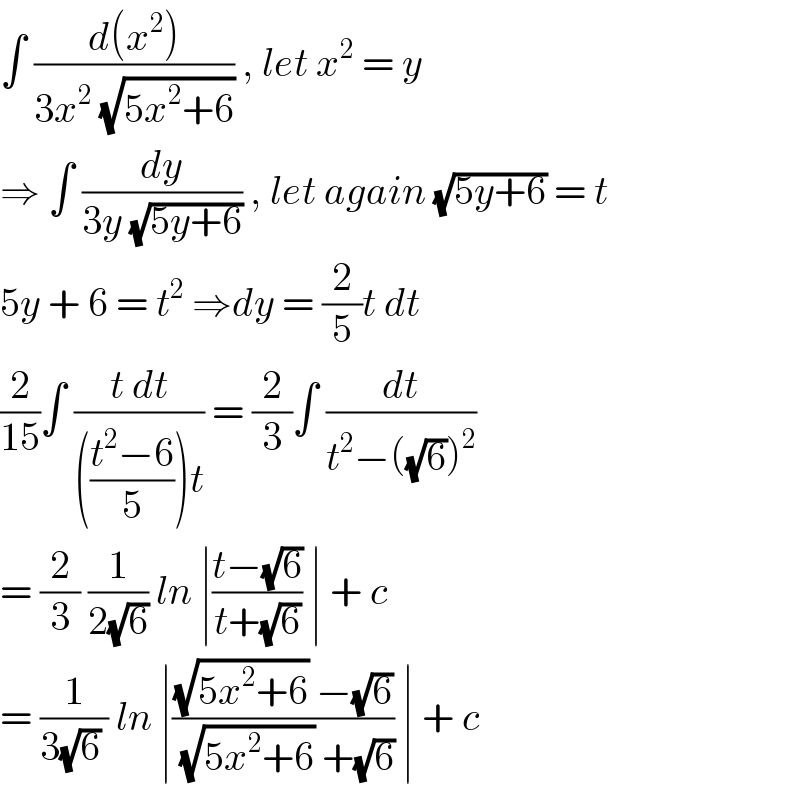
$$\int\:\frac{{d}\left({x}^{\mathrm{2}} \right)}{\mathrm{3}{x}^{\mathrm{2}} \:\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{6}}}\:,\:{let}\:{x}^{\mathrm{2}} \:=\:{y} \\ $$$$\Rightarrow\:\int\:\frac{{dy}}{\mathrm{3}{y}\:\sqrt{\mathrm{5}{y}+\mathrm{6}}}\:,\:{let}\:{again}\:\sqrt{\mathrm{5}{y}+\mathrm{6}}\:=\:{t} \\ $$$$\mathrm{5}{y}\:+\:\mathrm{6}\:=\:{t}^{\mathrm{2}} \:\Rightarrow{dy}\:=\:\frac{\mathrm{2}}{\mathrm{5}}{t}\:{dt}\: \\ $$$$\frac{\mathrm{2}}{\mathrm{15}}\int\:\frac{{t}\:{dt}}{\left(\frac{{t}^{\mathrm{2}} −\mathrm{6}}{\mathrm{5}}\right){t}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{{dt}}{{t}^{\mathrm{2}} −\left(\sqrt{\mathrm{6}}\right)^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\:{ln}\:\mid\frac{{t}−\sqrt{\mathrm{6}}}{{t}+\sqrt{\mathrm{6}}}\:\mid\:+\:{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{6}}\:}\:{ln}\:\mid\frac{\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{6}}\:−\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{6}}\:+\sqrt{\mathrm{6}}}\:\mid\:+\:{c}\: \\ $$
Commented by jagoll last updated on 23/Feb/20
$${waw}\:{creatif}\:{sir}.\:{thank}\:{you} \\ $$
Commented by mathmax by abdo last updated on 23/Feb/20

$${let}\:{I}\:=\:\int\:\frac{\mathrm{2}{dx}}{\mathrm{3}{x}\sqrt{\mathrm{5}{x}^{\mathrm{2}} \:+\mathrm{6}}}\:\Rightarrow\frac{\mathrm{3}}{\mathrm{2}}{I}\:=\int\:\:\frac{{dx}}{{x}\sqrt{\mathrm{5}\left({x}^{\mathrm{2}} \:+\frac{\mathrm{6}}{\mathrm{5}}\right)}} \\ $$$$=_{{x}=\sqrt{\frac{\mathrm{6}}{\mathrm{5}\:}}{u}} \:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\int\:\:\:\frac{\sqrt{\frac{\mathrm{6}}{\mathrm{5}}}{du}}{\:\sqrt{\frac{\mathrm{6}}{\mathrm{5}}}{u}×\sqrt{\frac{\mathrm{6}}{\mathrm{5}}}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}×\frac{\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{6}}}\:\int\:\:\frac{{du}}{{u}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:\int\:\:\frac{{du}}{{u}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}\:=_{{u}={sh}\left({z}\right)} \:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:\int\:\:\frac{{ch}\left({z}\right)}{{sh}\left({z}\right){ch}\left({z}\right)}{dz} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\int\:\:\frac{{dz}}{\frac{{e}^{{z}} −{e}^{−{z}} }{\mathrm{2}}}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}}\:\int\:\:\frac{{dz}}{{e}^{{z}} −{e}^{−{z}} }\:=_{{e}^{{z}} =\alpha} \:\:\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}}\int\:\:\frac{{d}\alpha}{\alpha\left(\alpha−\alpha^{−\mathrm{1}} \right)} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}}\:\int\:\frac{{d}\alpha}{\alpha^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\int\:\left(\frac{\mathrm{1}}{\alpha−\mathrm{1}}−\frac{\mathrm{1}}{\alpha+\mathrm{1}}\right){d}\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}{ln}\mid\frac{\alpha−\mathrm{1}}{\alpha+\mathrm{1}}\mid\:+{C} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}{ln}\mid\frac{{e}^{{z}} −\mathrm{1}}{{e}^{{z}} \:+\mathrm{1}}\mid\:+{C}\:{we}\:{have}\:{z}\:={argsh}\left({u}\right)={ln}\left(\mathrm{1}+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${e}^{{z}} =\mathrm{1}+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }=\mathrm{1}+\sqrt{\mathrm{1}+\left(\sqrt{\frac{\mathrm{5}}{\mathrm{6}}}{u}\right)^{\mathrm{2}} }=\mathrm{1}+\sqrt{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{6}}{u}^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}{ln}\mid\frac{\sqrt{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{6}}{u}^{\mathrm{2}} }}{\mathrm{2}+\sqrt{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{6}}{u}^{\mathrm{2}} }}\mid\:+{C} \\ $$
Commented by mathmax by abdo last updated on 23/Feb/20
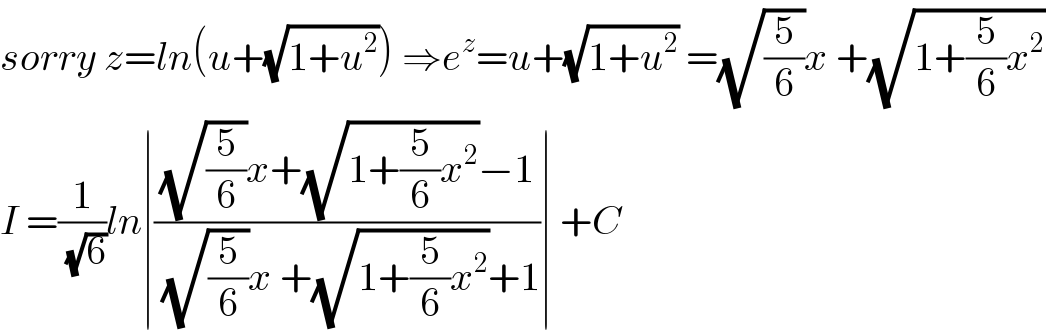
$${sorry}\:{z}={ln}\left({u}+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\right)\:\Rightarrow{e}^{{z}} ={u}+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\:=\sqrt{\frac{\mathrm{5}}{\mathrm{6}}}{x}\:+\sqrt{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{6}}{x}^{\mathrm{2}} } \\ $$$${I}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}{ln}\mid\frac{\sqrt{\frac{\mathrm{5}}{\mathrm{6}}}{x}+\sqrt{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{6}}{x}^{\mathrm{2}} }−\mathrm{1}}{\:\sqrt{\frac{\mathrm{5}}{\mathrm{6}}}{x}\:+\sqrt{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{6}}{x}^{\mathrm{2}} }+\mathrm{1}}\mid\:+{C} \\ $$
Answered by TANMAY PANACEA last updated on 23/Feb/20
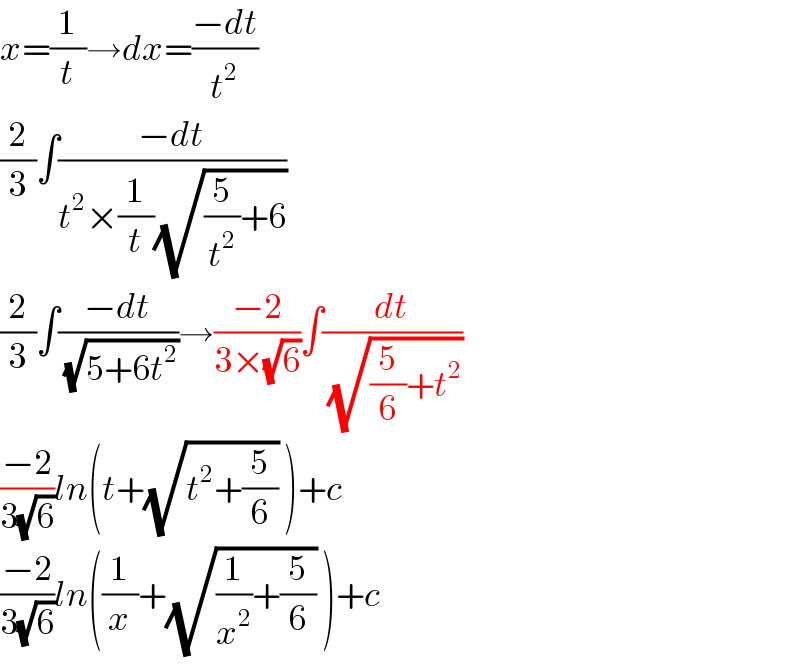
$${x}=\frac{\mathrm{1}}{{t}}\rightarrow{dx}=\frac{−{dt}}{{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{−{dt}}{{t}^{\mathrm{2}} ×\frac{\mathrm{1}}{{t}}\sqrt{\frac{\mathrm{5}}{{t}^{\mathrm{2}} }+\mathrm{6}}} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{−{dt}}{\:\sqrt{\mathrm{5}+\mathrm{6}{t}^{\mathrm{2}} }}\rightarrow\frac{−\mathrm{2}}{\mathrm{3}×\sqrt{\mathrm{6}}}\int\frac{{dt}}{\:\sqrt{\frac{\mathrm{5}}{\mathrm{6}}+{t}^{\mathrm{2}} }} \\ $$$$\frac{−\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{6}}}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{6}}}\:\right)+{c} \\ $$$$\frac{−\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{6}}}{ln}\left(\frac{\mathrm{1}}{{x}}+\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{5}}{\mathrm{6}}}\:\right)+{c} \\ $$
Commented by jagoll last updated on 23/Feb/20

$${thank}\:{you}\:{sir} \\ $$
