Question Number 54556 by gunawan last updated on 06/Feb/19
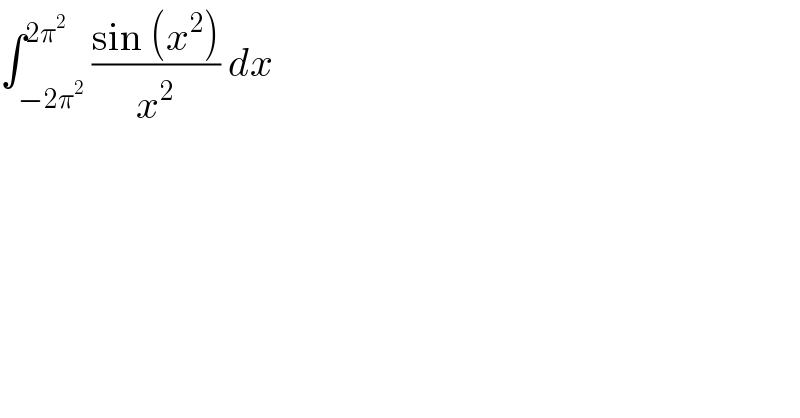
$$\int_{−\mathrm{2}\pi^{\mathrm{2}} } ^{\mathrm{2}\pi^{\mathrm{2}} } \frac{\mathrm{sin}\:\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }\:{dx} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Feb/19

Commented by tanmay.chaudhury50@gmail.com last updated on 06/Feb/19

Commented by gunawan last updated on 06/Feb/19

$$\mathrm{thank}\:\mathrm{You}\:\mathrm{Sir} \\ $$
Commented by maxmathsup by imad last updated on 06/Feb/19
![let I =∫_(−2π^2 ) ^(2π^2 ) ((sin(x^2 ))/x^2 )dx ⇒ I =2 ∫_0 ^(2π^2 ) ((sin(x^2 ))/x^2 )dx by psrts ∫_0 ^(2π^2 ) ((sin(x^2 ))/x^2 )dx =[−(1/x)sin(x^2 )]_0 ^(2π^2 ) −∫_0 ^(2π^2 ) (−(1/x))2x cos(x^2 ) dx =−(1/(2π^2 ))sin(4π^4 )+ 2 ∫_0 ^(2π^2 ) cos(x^2 )dx but we have cosu =Σ_(n=0) ^∞ (((−1)^n u^(2n) )/((2n)!)) ⇒ cos(x^2 ) =Σ_(n=0) ^∞ (((−1)^n x^(4n) )/((2n)!)) ⇒ ∫_0 ^(2π^2 ) cos(x^2 )dx =Σ_(n=0) ^∞ (((−1)^n )/((2n)!)) ∫_0 ^(2π^2 ) x^(4n) dx =Σ_(n=0) ^∞ (((−1)^n )/((2n)!)) (1/(4n+1))(2π^2 )^(4n+1) =Σ_(n=0) ^∞ (((−1)^n )/((2n)!(4n+1))) 2^(4n+1) π^(8n+2) ⇒ I =Σ_(n=0) ^∞ (((−1)^n )/((2n)!(4n+1))) 2^(4n+3) π^(8n+2) −((sin(4π^4 ))/π^2 ) I is given at form of serie .](https://www.tinkutara.com/question/Q54564.png)
$${let}\:{I}\:=\int_{−\mathrm{2}\pi^{\mathrm{2}} } ^{\mathrm{2}\pi^{\mathrm{2}} } \:\:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\:\Rightarrow\:{I}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi^{\mathrm{2}} } \:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\:\:\:{by}\:{psrts} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi^{\mathrm{2}} } \:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\:=\left[−\frac{\mathrm{1}}{{x}}{sin}\left({x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi^{\mathrm{2}} } \:−\int_{\mathrm{0}} ^{\mathrm{2}\pi^{\mathrm{2}} } \left(−\frac{\mathrm{1}}{{x}}\right)\mathrm{2}{x}\:{cos}\left({x}^{\mathrm{2}} \right)\:{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\pi^{\mathrm{2}} }{sin}\left(\mathrm{4}\pi^{\mathrm{4}} \right)+\:\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi^{\mathrm{2}} } \:{cos}\left({x}^{\mathrm{2}} \right){dx}\:\:\:{but}\:{we}\:{have}\: \\ $$$${cosu}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:{u}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\:\Rightarrow\:{cos}\left({x}^{\mathrm{2}} \right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{4}{n}} }{\left(\mathrm{2}{n}\right)!}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi^{\mathrm{2}} } \:{cos}\left({x}^{\mathrm{2}} \right){dx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right)!}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi^{\mathrm{2}} } {x}^{\mathrm{4}{n}} {dx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right)!}\:\frac{\mathrm{1}}{\mathrm{4}{n}+\mathrm{1}}\left(\mathrm{2}\pi^{\mathrm{2}} \right)^{\mathrm{4}{n}+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right)!\left(\mathrm{4}{n}+\mathrm{1}\right)}\:\mathrm{2}^{\mathrm{4}{n}+\mathrm{1}} \:\pi^{\mathrm{8}{n}+\mathrm{2}} \:\:\Rightarrow \\ $$$${I}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right)!\left(\mathrm{4}{n}+\mathrm{1}\right)}\:\mathrm{2}^{\mathrm{4}{n}+\mathrm{3}} \:\pi^{\mathrm{8}{n}+\mathrm{2}} −\frac{{sin}\left(\mathrm{4}\pi^{\mathrm{4}} \right)}{\pi^{\mathrm{2}} } \\ $$$${I}\:{is}\:{given}\:{at}\:{form}\:{of}\:{serie}\:. \\ $$
