Question Number 20388 by tammi last updated on 26/Aug/17

$$\int\frac{\mathrm{2sin}\:{x}+\mathrm{3cos}\:{x}}{\mathrm{7sin}\:{x}−\mathrm{2cos}\:{x}} \\ $$
Answered by $@ty@m last updated on 26/Aug/17
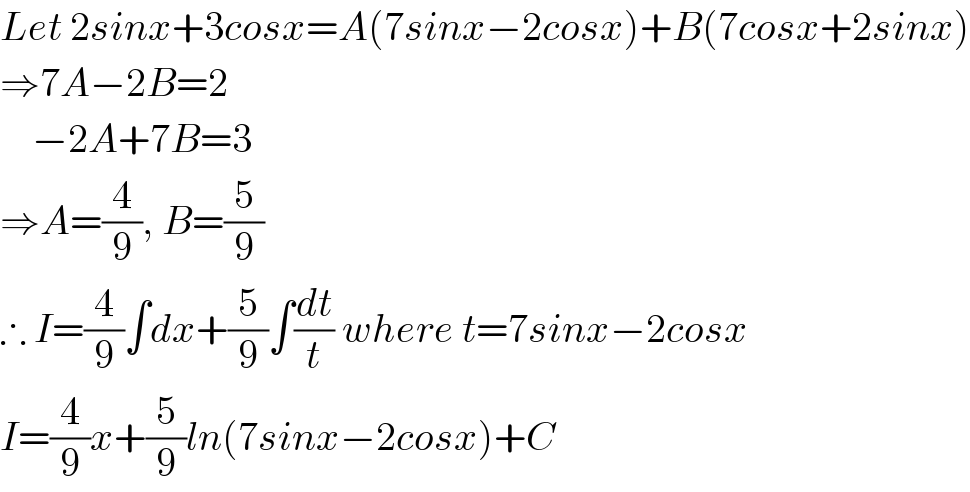
$${Let}\:\mathrm{2}{sinx}+\mathrm{3}{cosx}={A}\left(\mathrm{7}{sinx}−\mathrm{2}{cosx}\right)+{B}\left(\mathrm{7}{cosx}+\mathrm{2}{sinx}\right) \\ $$$$\Rightarrow\mathrm{7}{A}−\mathrm{2}{B}=\mathrm{2} \\ $$$$\:\:\:\:−\mathrm{2}{A}+\mathrm{7}{B}=\mathrm{3} \\ $$$$\Rightarrow{A}=\frac{\mathrm{4}}{\mathrm{9}},\:{B}=\frac{\mathrm{5}}{\mathrm{9}} \\ $$$$\therefore\:{I}=\frac{\mathrm{4}}{\mathrm{9}}\int{dx}+\frac{\mathrm{5}}{\mathrm{9}}\int\frac{{dt}}{{t}}\:{where}\:{t}=\mathrm{7}{sinx}−\mathrm{2}{cosx} \\ $$$${I}=\frac{\mathrm{4}}{\mathrm{9}}{x}+\frac{\mathrm{5}}{\mathrm{9}}{ln}\left(\mathrm{7}{sinx}−\mathrm{2}{cosx}\right)+{C} \\ $$
