Question Number 94735 by student work last updated on 20/May/20

$$\int\frac{\mathrm{2t}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{4}} \right)\left(\mathrm{1}+\mathrm{t}\right)}\mathrm{dt}=? \\ $$
Commented by student work last updated on 20/May/20

$$\mathrm{who}\:\mathrm{can}\:\mathrm{another}? \\ $$
Commented by student work last updated on 20/May/20

$$\mathrm{who}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{describly}? \\ $$
Commented by MJS last updated on 20/May/20

$$\mathrm{are}\:\mathrm{you}\:\mathrm{able}\:\mathrm{to}\:\mathrm{decompose}?\:\mathrm{I}\:\mathrm{gave}\:\mathrm{you} \\ $$$$\mathrm{enough}\:\mathrm{hints}.\:\mathrm{if}\:\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{decomposition} \\ $$$$\mathrm{start}\:\mathrm{with}\:\mathrm{some}\:\mathrm{easier}\:\mathrm{examples}. \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{tired}\:\mathrm{of}\:\mathrm{typing}\:\mathrm{obvious}\:\mathrm{things}. \\ $$
Commented by student work last updated on 20/May/20

$$\mathrm{why}\:\mathrm{you}\:\mathrm{not}\:\mathrm{solve}? \\ $$
Commented by MJS last updated on 20/May/20

$$\mathrm{I}\:\mathrm{solved}\:\mathrm{it}.\:\mathrm{Question}\:\mathrm{94574} \\ $$$$\mathrm{I}\:\mathrm{decomposed}\:\mathrm{it}\:\mathrm{in}\:\mathrm{2}\:\mathrm{steps}.\:\mathrm{what}\:\mathrm{else}\:\mathrm{do}\:\mathrm{you} \\ $$$$\mathrm{want}? \\ $$
Commented by Tony Lin last updated on 21/May/20

$$\int\frac{\mathrm{2}{t}}{\left(\mathrm{1}+{t}^{\mathrm{4}} \right)\left(\mathrm{1}+{t}\right)}{dt} \\ $$$$=\int\:\frac{{t}^{\mathrm{3}} −{t}^{\mathrm{2}} +{t}+\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{4}} }{dt}−\int\frac{\mathrm{1}}{\mathrm{1}+{t}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(\int\:\frac{\left(\sqrt{\mathrm{2}}+\mathrm{2}\right){t}+\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt}+\int\frac{\left(\sqrt{\mathrm{2}}−\mathrm{2}\right){t}+\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt}\right)−\int\frac{\mathrm{1}}{\mathrm{1}+{t}}{dt} \\ $$$${now}\:{it}\:{is}\:{easy}\:{to}\:{solve} \\ $$$${it}\:{can}\:{be}\:{expressed}\:{by}\:{ln}\:{and}\:{arctan} \\ $$
Commented by student work last updated on 21/May/20

$$\mathrm{explain}\:\mathrm{me} \\ $$
Commented by MJS last updated on 21/May/20
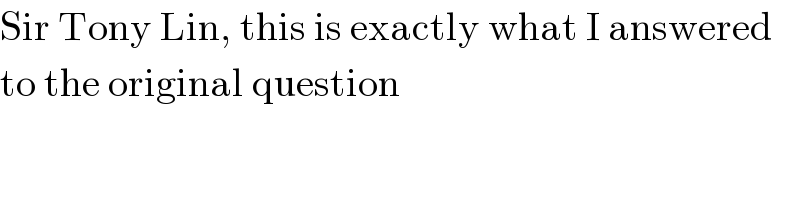
$$\mathrm{Sir}\:\mathrm{Tony}\:\mathrm{Lin},\:\mathrm{this}\:\mathrm{is}\:\mathrm{exactly}\:\mathrm{what}\:\mathrm{I}\:\mathrm{answered} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{original}\:\mathrm{question} \\ $$
Commented by MJS last updated on 21/May/20

$$\mathrm{Sir}\:\mathrm{student}\:\mathrm{work},\:\mathrm{if}\:\mathrm{you}\:\mathrm{cannot}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{from} \\ $$$$\mathrm{there},\:\mathrm{better}\:\mathrm{start}\:\mathrm{learning}\:\mathrm{basic}\:\mathrm{integrals}. \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{use}\:\mathrm{solving}\:\mathrm{problems}\:\mathrm{like}\:\mathrm{this}\:\mathrm{one} \\ $$$$\mathrm{for}\:\mathrm{you}\:\mathrm{if}\:\mathrm{you}\:\mathrm{cannot}\:\mathrm{understand}\:\mathrm{each}\:\mathrm{simple} \\ $$$$\mathrm{step}. \\ $$
