Question Number 42170 by lucha116 last updated on 19/Aug/18
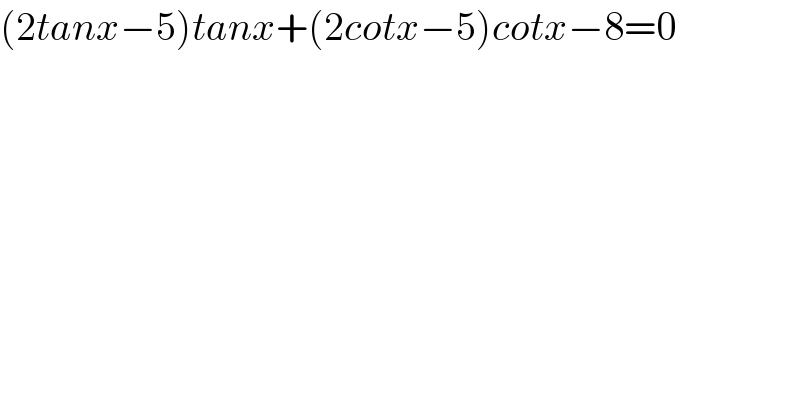
$$\left(\mathrm{2}{tanx}−\mathrm{5}\right){tanx}+\left(\mathrm{2}{cotx}−\mathrm{5}\right){cotx}−\mathrm{8}=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Aug/18
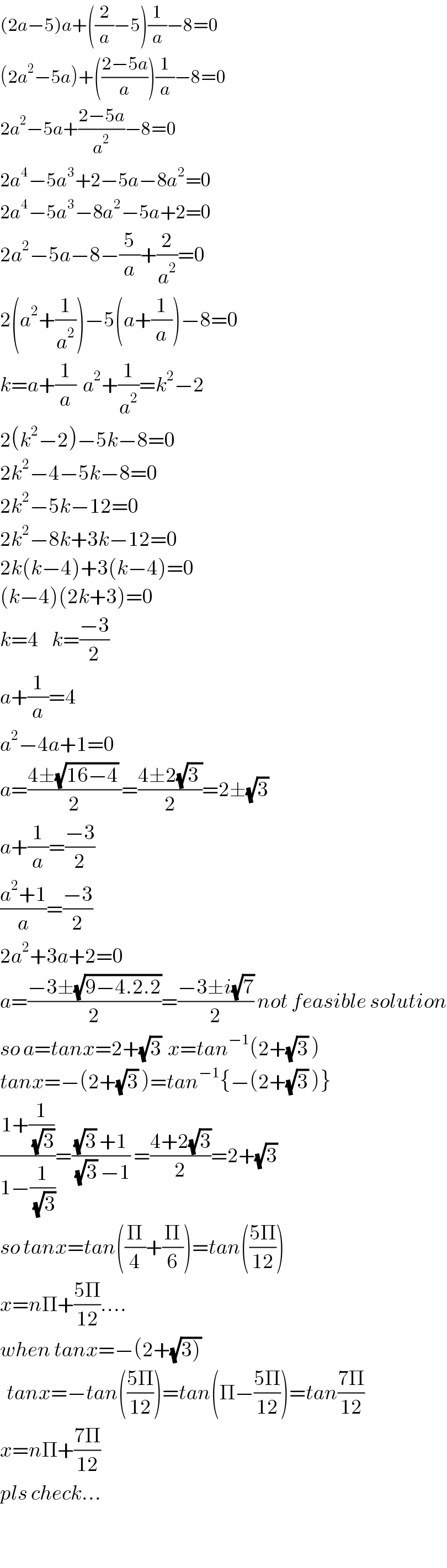
$$\left(\mathrm{2}{a}−\mathrm{5}\right){a}+\left(\frac{\mathrm{2}}{{a}}−\mathrm{5}\right)\frac{\mathrm{1}}{{a}}−\mathrm{8}=\mathrm{0} \\ $$$$\left(\mathrm{2}{a}^{\mathrm{2}} −\mathrm{5}{a}\right)+\left(\frac{\mathrm{2}−\mathrm{5}{a}}{{a}}\right)\frac{\mathrm{1}}{{a}}−\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} −\mathrm{5}{a}+\frac{\mathrm{2}−\mathrm{5}{a}}{{a}^{\mathrm{2}} }−\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{2}{a}^{\mathrm{4}} −\mathrm{5}{a}^{\mathrm{3}} +\mathrm{2}−\mathrm{5}{a}−\mathrm{8}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2}{a}^{\mathrm{4}} −\mathrm{5}{a}^{\mathrm{3}} −\mathrm{8}{a}^{\mathrm{2}} −\mathrm{5}{a}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} −\mathrm{5}{a}−\mathrm{8}−\frac{\mathrm{5}}{{a}}+\frac{\mathrm{2}}{{a}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\mathrm{2}\left({a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)−\mathrm{5}\left({a}+\frac{\mathrm{1}}{{a}}\right)−\mathrm{8}=\mathrm{0} \\ $$$${k}={a}+\frac{\mathrm{1}}{{a}}\:\:{a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }={k}^{\mathrm{2}} −\mathrm{2} \\ $$$$\mathrm{2}\left({k}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{5}{k}−\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{2}{k}^{\mathrm{2}} −\mathrm{4}−\mathrm{5}{k}−\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{2}{k}^{\mathrm{2}} −\mathrm{5}{k}−\mathrm{12}=\mathrm{0} \\ $$$$\mathrm{2}{k}^{\mathrm{2}} −\mathrm{8}{k}+\mathrm{3}{k}−\mathrm{12}=\mathrm{0} \\ $$$$\mathrm{2}{k}\left({k}−\mathrm{4}\right)+\mathrm{3}\left({k}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\left({k}−\mathrm{4}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)=\mathrm{0} \\ $$$${k}=\mathrm{4}\:\:\:\:{k}=\frac{−\mathrm{3}}{\mathrm{2}} \\ $$$${a}+\frac{\mathrm{1}}{{a}}=\mathrm{4} \\ $$$${a}^{\mathrm{2}} −\mathrm{4}{a}+\mathrm{1}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}}\:}{\mathrm{2}}=\frac{\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{3}\:}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$${a}+\frac{\mathrm{1}}{{a}}=\frac{−\mathrm{3}}{\mathrm{2}} \\ $$$$\frac{{a}^{\mathrm{2}} +\mathrm{1}}{{a}}=\frac{−\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} +\mathrm{3}{a}+\mathrm{2}=\mathrm{0} \\ $$$${a}=\frac{−\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{4}.\mathrm{2}.\mathrm{2}}}{\mathrm{2}}=\frac{−\mathrm{3}\pm{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\:{not}\:{feasible}\:{solution} \\ $$$${so}\:{a}={tanx}=\mathrm{2}+\sqrt{\mathrm{3}}\:\:{x}={tan}^{−\mathrm{1}} \left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right) \\ $$$${tanx}=−\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)={tan}^{−\mathrm{1}} \left\{−\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)\right\} \\ $$$$\frac{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}=\frac{\sqrt{\mathrm{3}}\:+\mathrm{1}}{\:\sqrt{\mathrm{3}}\:−\mathrm{1}}\:=\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$${so}\:{tanx}={tan}\left(\frac{\Pi}{\mathrm{4}}+\frac{\Pi}{\mathrm{6}}\right)={tan}\left(\frac{\mathrm{5}\Pi}{\mathrm{12}}\right) \\ $$$${x}={n}\Pi+\frac{\mathrm{5}\Pi}{\mathrm{12}}…. \\ $$$${when}\:{tanx}=−\left(\mathrm{2}+\sqrt{\left.\mathrm{3}\right)}\right. \\ $$$$\:\:{tanx}=−{tan}\left(\frac{\mathrm{5}\Pi}{\mathrm{12}}\right)={tan}\left(\Pi−\frac{\mathrm{5}\Pi}{\mathrm{12}}\right)={tan}\frac{\mathrm{7}\Pi}{\mathrm{12}} \\ $$$${x}={n}\Pi+\frac{\mathrm{7}\Pi}{\mathrm{12}} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$
Commented by lucha116 last updated on 20/Aug/18
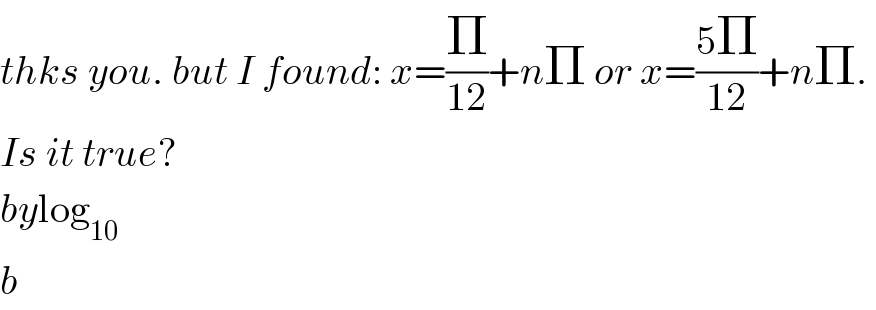
$${thks}\:{you}.\:{but}\:{I}\:{found}:\:{x}=\frac{\Pi}{\mathrm{12}}+{n}\Pi\:{or}\:{x}=\frac{\mathrm{5}\Pi}{\mathrm{12}}+{n}\Pi.\: \\ $$$${Is}\:{it}\:{true}? \\ $$$${by}\mathrm{log}_{\mathrm{10}} \\ $$$${b} \\ $$
