Question Number 81279 by jagoll last updated on 11/Feb/20
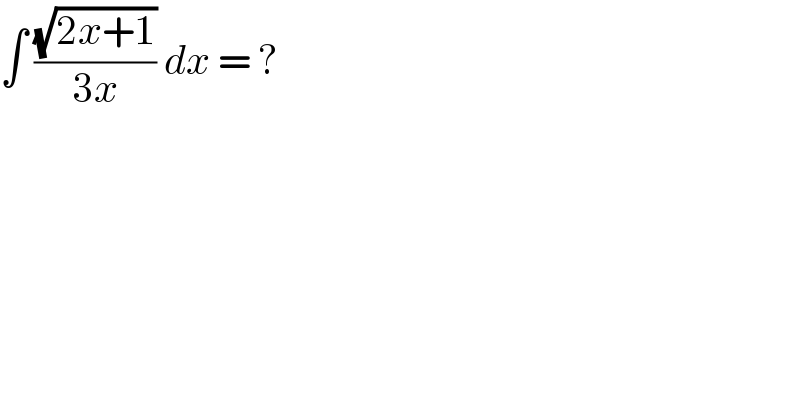
$$\int\:\frac{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{\mathrm{3}{x}}\:{dx}\:=\:? \\ $$
Commented by john santu last updated on 11/Feb/20
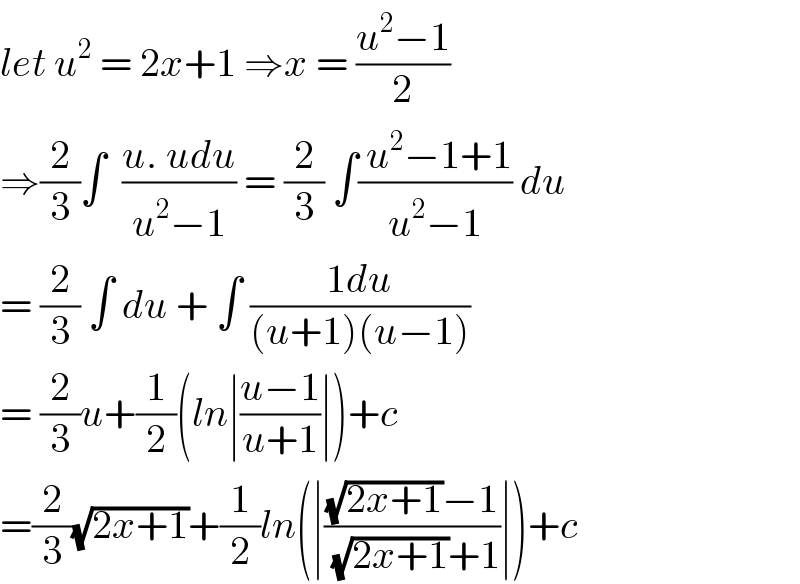
$${let}\:{u}^{\mathrm{2}} \:=\:\mathrm{2}{x}+\mathrm{1}\:\Rightarrow{x}\:=\:\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{3}}\int\:\:\frac{{u}.\:{udu}}{{u}^{\mathrm{2}} −\mathrm{1}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\int\frac{\:{u}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{u}^{\mathrm{2}} −\mathrm{1}}\:{du} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}\:\int\:{du}\:+\:\int\:\frac{\mathrm{1}{du}}{\left({u}+\mathrm{1}\right)\left({u}−\mathrm{1}\right)} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}{u}+\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid\right)+{c} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{2}{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mid\frac{\sqrt{\mathrm{2}{x}+\mathrm{1}}−\mathrm{1}}{\:\sqrt{\mathrm{2}{x}+\mathrm{1}}+\mathrm{1}}\mid\right)+{c} \\ $$
Commented by jagoll last updated on 11/Feb/20
$${thank}\:{you}\:{mister} \\ $$
