Question Number 57164 by ANTARES VY last updated on 31/Mar/19
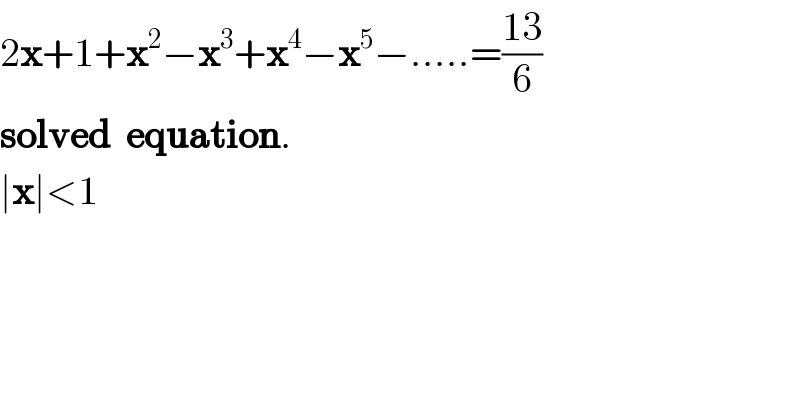
$$\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\boldsymbol{\mathrm{x}}^{\mathrm{4}} −\boldsymbol{\mathrm{x}}^{\mathrm{5}} −…..=\frac{\mathrm{13}}{\mathrm{6}} \\ $$$$\boldsymbol{\mathrm{solved}}\:\:\boldsymbol{\mathrm{equation}}. \\ $$$$\mid\boldsymbol{\mathrm{x}}\mid<\mathrm{1} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 31/Mar/19
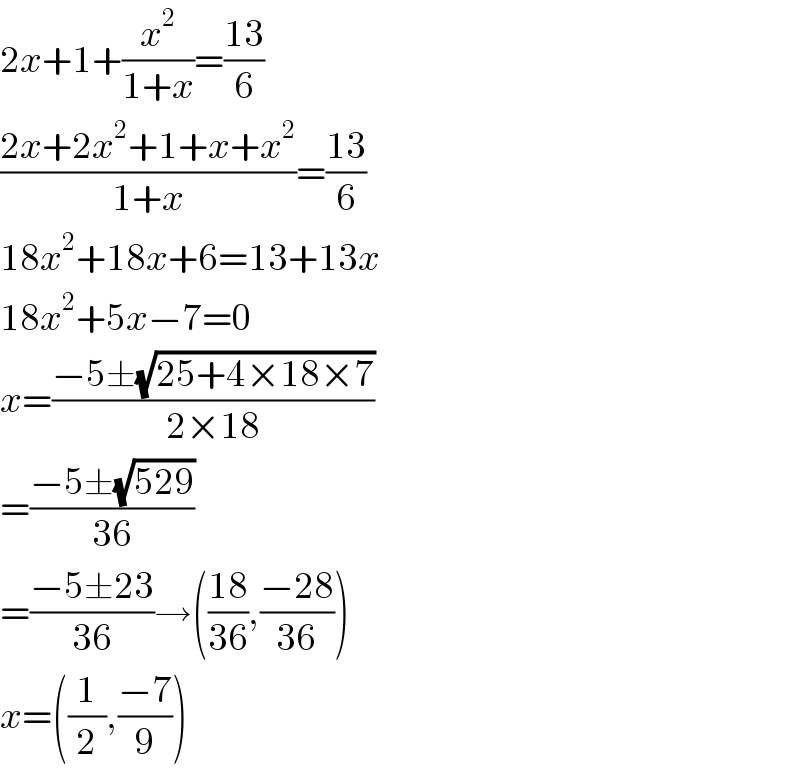
$$\mathrm{2}{x}+\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}}=\frac{\mathrm{13}}{\mathrm{6}} \\ $$$$\frac{\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}+{x}+{x}^{\mathrm{2}} }{\mathrm{1}+{x}}=\frac{\mathrm{13}}{\mathrm{6}} \\ $$$$\mathrm{18}{x}^{\mathrm{2}} +\mathrm{18}{x}+\mathrm{6}=\mathrm{13}+\mathrm{13}{x} \\ $$$$\mathrm{18}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{7}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{5}\pm\sqrt{\mathrm{25}+\mathrm{4}×\mathrm{18}×\mathrm{7}}}{\mathrm{2}×\mathrm{18}} \\ $$$$=\frac{−\mathrm{5}\pm\sqrt{\mathrm{529}}}{\mathrm{36}} \\ $$$$=\frac{−\mathrm{5}\pm\mathrm{23}}{\mathrm{36}}\rightarrow\left(\frac{\mathrm{18}}{\mathrm{36}},\frac{−\mathrm{28}}{\mathrm{36}}\right) \\ $$$${x}=\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{−\mathrm{7}}{\mathrm{9}}\right) \\ $$
