Question Number 161068 by blackmamba last updated on 11/Dec/21
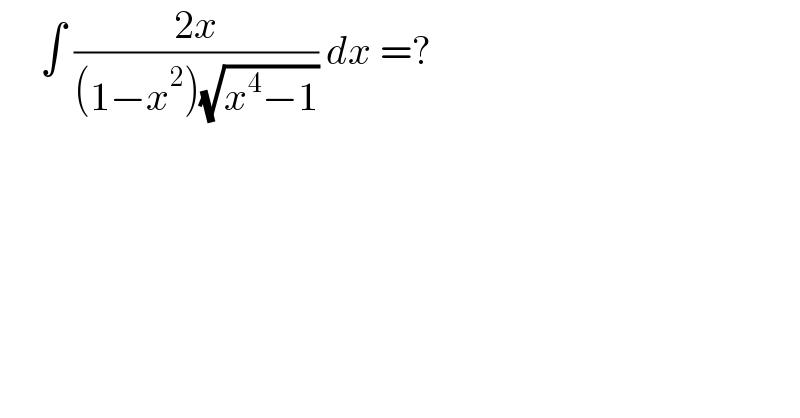
$$\:\:\:\:\:\int\:\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}}\:{dx}\:=? \\ $$
Answered by chhaythean last updated on 11/Dec/21
![=−∫((2x)/((x^2 −1)(√(x^4 −1))))dx =−∫((2x)/((x^2 −1)[(x^2 −1)(x^2 +1)]^(1/2) ))dx =−∫((2x)/((x^2 −1)^2 [(((x^2 +1))/((x^2 −1)))]^(1/2) ))dx let u=(((x^2 +1))/((x^2 −1)))⇒du=((−4x)/((x^2 −1)^2 ))dx =(1/2)∫(du/( (√u)))=(√u)+c =(√((x^2 +1)/(x^2 −1)))+c So determinant (((∫((2x)/((1−x^2 )(√(x^4 −1))))dx=(√((x^2 +1)/(x^2 −1)))+c)))](https://www.tinkutara.com/question/Q161070.png)
$$=−\int\frac{\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{4}} −\mathrm{1}}}\mathrm{dx} \\ $$$$=−\int\frac{\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\left[\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\right]^{\frac{\mathrm{1}}{\mathrm{2}}} }\mathrm{dx} \\ $$$$=−\int\frac{\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \left[\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)}\right]^{\frac{\mathrm{1}}{\mathrm{2}}} }\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{u}=\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)}\Rightarrow\mathrm{du}=\frac{−\mathrm{4x}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{du}}{\:\sqrt{\mathrm{u}}}=\sqrt{\mathrm{u}}+\mathrm{c} \\ $$$$=\sqrt{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}+\mathrm{c} \\ $$$$\mathrm{So}\:\begin{array}{|c|}{\int\frac{\mathrm{2x}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\sqrt{\mathrm{x}^{\mathrm{4}} −\mathrm{1}}}\mathrm{dx}=\sqrt{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}+\mathrm{c}}\\\hline\end{array} \\ $$
Answered by Ar Brandon last updated on 11/Dec/21
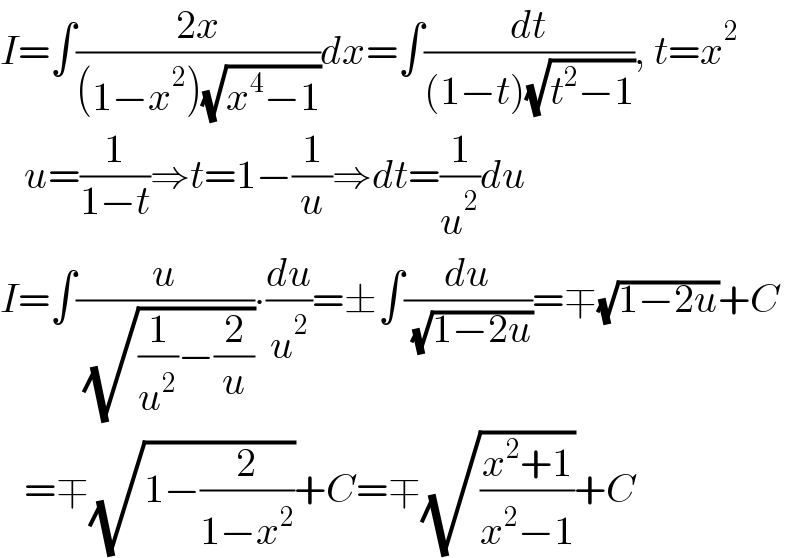
$${I}=\int\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}}{dx}=\int\frac{{dt}}{\left(\mathrm{1}−{t}\right)\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}},\:{t}={x}^{\mathrm{2}} \\ $$$$\:\:\:{u}=\frac{\mathrm{1}}{\mathrm{1}−{t}}\Rightarrow{t}=\mathrm{1}−\frac{\mathrm{1}}{{u}}\Rightarrow{dt}=\frac{\mathrm{1}}{{u}^{\mathrm{2}} }{du} \\ $$$${I}=\int\frac{{u}}{\:\sqrt{\frac{\mathrm{1}}{{u}^{\mathrm{2}} }−\frac{\mathrm{2}}{{u}}}}\centerdot\frac{{du}}{{u}^{\mathrm{2}} }=\pm\int\frac{{du}}{\:\sqrt{\mathrm{1}−\mathrm{2}{u}}}=\mp\sqrt{\mathrm{1}−\mathrm{2}{u}}+{C} \\ $$$$\:\:\:=\mp\sqrt{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1}−{x}^{\mathrm{2}} }}+{C}=\mp\sqrt{\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}}+{C} \\ $$
