Question Number 87185 by M±th+et£s last updated on 03/Apr/20

$$\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dx} \\ $$
Answered by peter frank last updated on 03/Apr/20
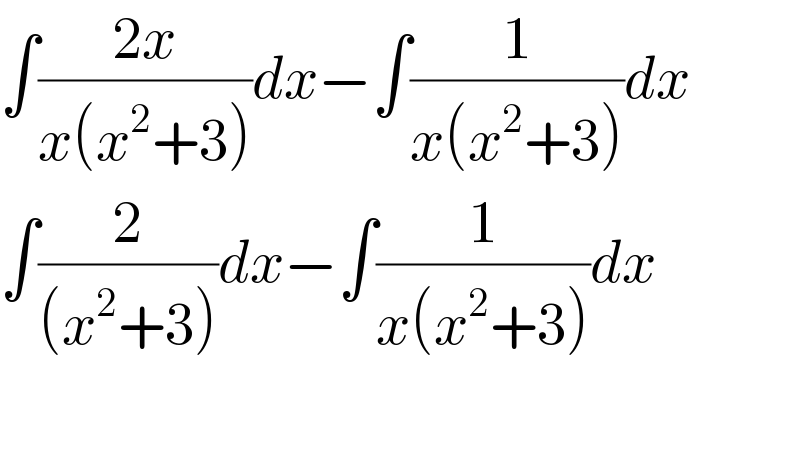
$$\int\frac{\mathrm{2}{x}}{{x}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dx}−\int\frac{\mathrm{1}}{{x}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dx} \\ $$$$\int\frac{\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dx}−\int\frac{\mathrm{1}}{{x}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dx} \\ $$$$ \\ $$
Answered by Kunal12588 last updated on 03/Apr/20

$$\frac{\mathrm{2}{x}−\mathrm{1}}{{x}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}=\frac{{a}}{{x}}+\frac{{bx}+{c}}{{x}^{\mathrm{2}} +\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2}{x}−\mathrm{1}=\left({a}+{b}\right){x}^{\mathrm{2}} +{cx}+\mathrm{3}{a} \\ $$$${a}=−\frac{\mathrm{1}}{\mathrm{3}},\:{b}=\frac{\mathrm{1}}{\mathrm{3}},\:{c}=\mathrm{2} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}\:{dx}}{{x}^{\mathrm{2}} +\mathrm{3}}+\mathrm{2}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{3}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mid{x}\mid+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\mid{x}^{\mathrm{2}} +\mathrm{3}\mid+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{\mathrm{3}}}+{C} \\ $$
Commented by M±th+et£s last updated on 03/Apr/20

$${thank}\:{uou}\:{sir} \\ $$
Answered by redmiiuser last updated on 03/Apr/20
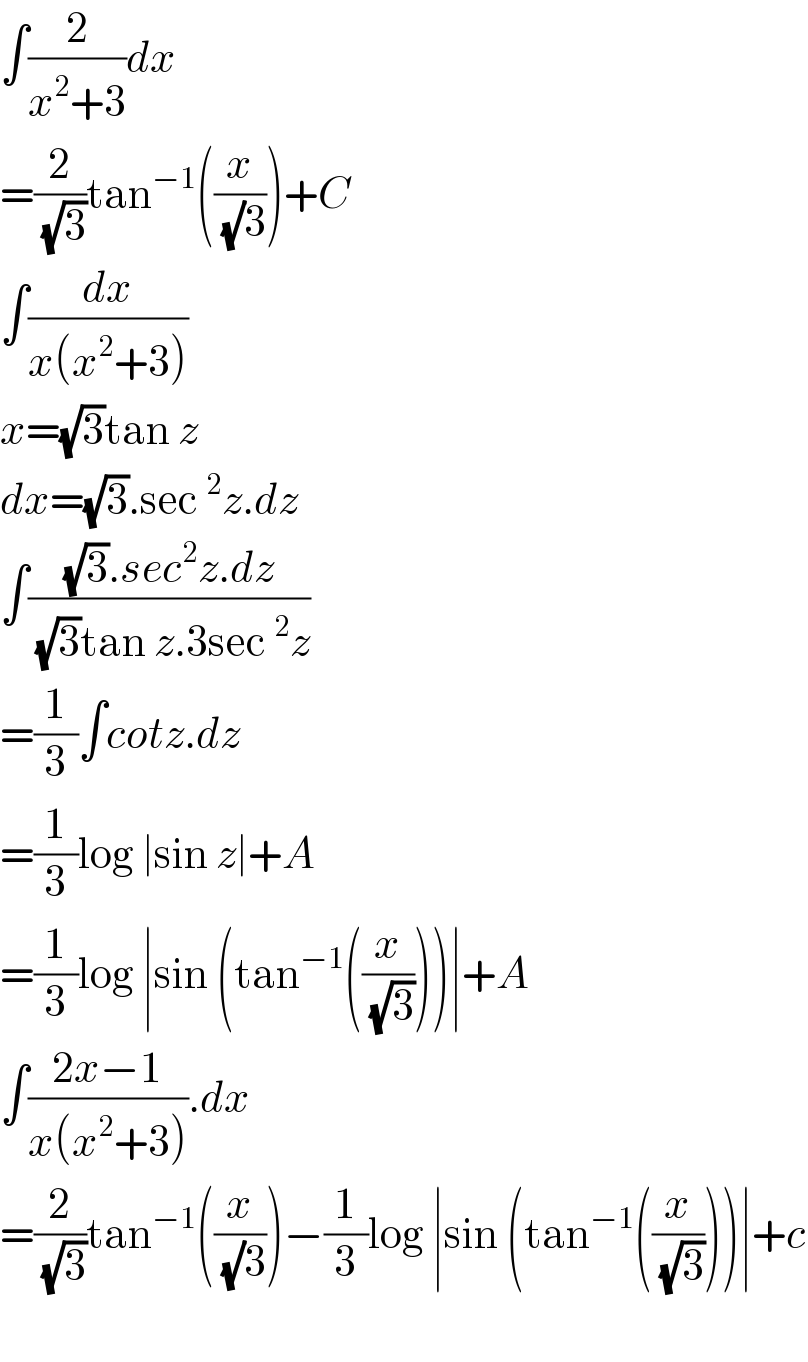
$$\int\frac{\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{3}}{dx} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{}\mathrm{3}}\right)+{C} \\ $$$$\int\frac{{dx}}{{x}\left({x}^{\mathrm{2}} +\mathrm{3}\right)} \\ $$$${x}=\sqrt{\mathrm{3}}\mathrm{tan}\:{z} \\ $$$${dx}=\sqrt{\mathrm{3}}.\mathrm{sec}\:^{\mathrm{2}} {z}.{dz} \\ $$$$\int\frac{\sqrt{\mathrm{3}}.{sec}^{\mathrm{2}} {z}.{dz}}{\:\sqrt{\mathrm{3}}\mathrm{tan}\:{z}.\mathrm{3sec}\:^{\mathrm{2}} {z}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int{cotz}.{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\:\mid\mathrm{sin}\:{z}\mid+{A} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\:\mid\mathrm{sin}\:\left(\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{3}}}\right)\right)\mid+{A} \\ $$$$\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}.{dx} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{}\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\:\mid\mathrm{sin}\:\left(\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{3}}}\right)\right)\mid+{c} \\ $$$$ \\ $$
Commented by redmiiuser last updated on 03/Apr/20

$${PLS}\:{CHECK} \\ $$
Commented by Joel578 last updated on 03/Apr/20

$${you}\:{can}\:{check}\:{by}\:{differentiating}\:{it}\:{again} \\ $$
Commented by M±th+et£s last updated on 03/Apr/20

$${nice}\:{solution}\:{sir} \\ $$
Commented by M±th+et£s last updated on 03/Apr/20

$${its}\:{didinte}\:{integeral}\:{if}\:{he}\:{derivative}\:{it}\:{the} \\ $$$${answer}\:{will}\:{be}\:{zero} \\ $$
Commented by M±th+et£s last updated on 03/Apr/20
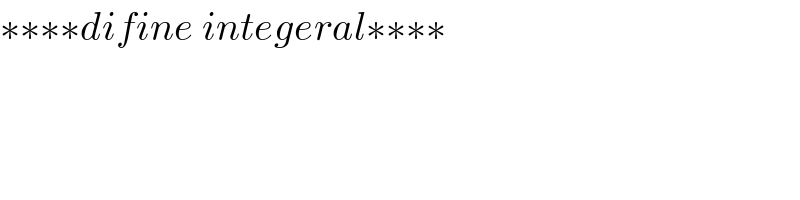
$$\ast\ast\ast\ast{difine}\:{integeral}\ast\ast\ast\ast \\ $$
