2x-2x-3-9-0-if-there-s-a-solution-to-equation-find-4a-3-

Question Number 147011 by mathdanisur last updated on 17/Jul/21

2 x - \sqrt{2 x - 3} - 9 = 0

i f {t h e r e}^{'} s a s o l u t i o n t o e q u a t i o n,

f i n d 4 a + 3 = ?

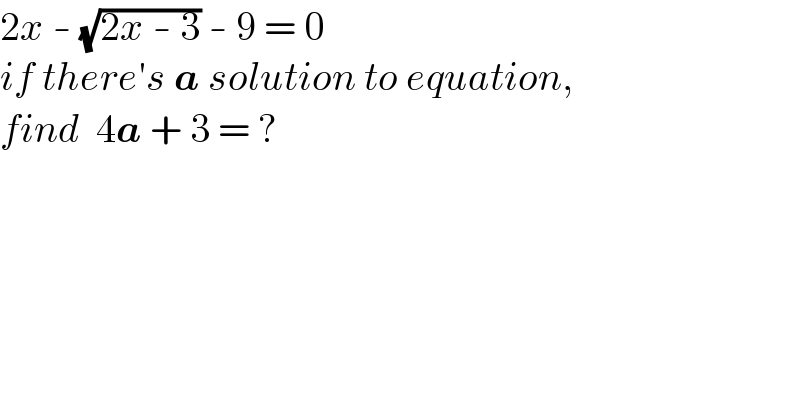
Commented by 7770 last updated on 17/Jul/21

4 x^{2} - 36 x + 81 - 2 x + 3 = 0

4 x^{2} - 38 x + 84 = 0

x_{1} = 6 x_{2} = 3.5

∴ 4 (3.5) + 3 = 17

4 (6) + 3 = 27

Commented by otchereabdullai@gmail.com last updated on 18/Jul/21

nice question

Commented by mathdanisur last updated on 18/Jul/21

t h a n k y o u S e r

Answered by gsk2684 last updated on 17/Jul/21

{(\sqrt{2 a - 3})}^{2} - \sqrt{2 a - 3} - 6 = 0

t^{2} - t - 6 = 0

(t - 3) (t + 2) = 0

t = 3

\sqrt{2 a - 3} = 3

2 a = 12

4 a + 3 = 27

Commented by mathdanisur last updated on 17/Jul/21

t h a n k y o u S e r, b u t a n s w e r 17

Commented by gsk2684 last updated on 17/Jul/21

i f s o t h e n a = \frac{17 - 3}{4} = \frac{14}{4} = \frac{7}{2}

2 a - \sqrt{2 a - 3} - 9

7 - 2 - 9

\neq 0

Commented by mathdanisur last updated on 18/Jul/21

t h a n k y o u S e r

Answered by Rasheed.Sindhi last updated on 17/Jul/21

2 x - \sqrt{2 x - 3} - 9 = 0

\underline{4 a + 3 = ? a : s o l u t i o n t o t h e e q u a t i o n}

4 x^{2} - 36 x + 81 = 2 x - 3

4 x^{2} - 38 x + 84 = 0

2 x^{2} - 19 x + 42 = 0

(x - 6) (2 x - 7) = 0

x = 6 \lor x = 7 / 2 (E x t a n e o u s r o o t)

a = 6

4 a + 3 = 4 (6) + 3 = 27

(I f x = 7 / 2 w e r e s a t i s f i e d

t h e n 4 a + 3 = 4 (\frac{7}{2}) + 3 = 17)

Commented by mathdanisur last updated on 17/Jul/21

t h a n k y o u S e r

Commented by mathdanisur last updated on 18/Jul/21

t h a n k y o u S e r