Question Number 115888 by Fikret last updated on 29/Sep/20
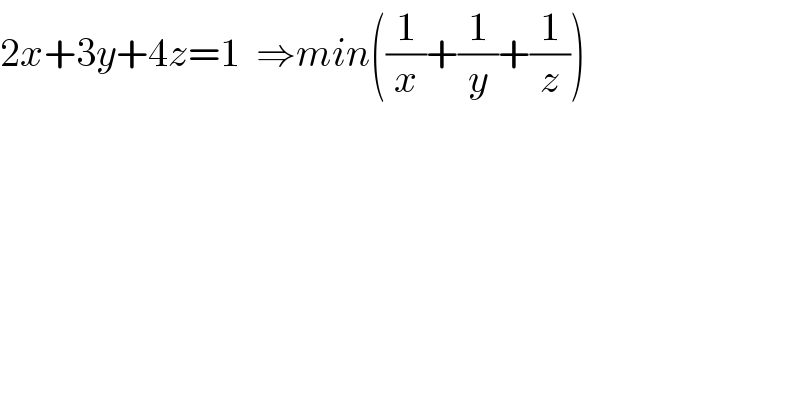
$$\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{4}{z}=\mathrm{1}\:\:\Rightarrow{min}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right) \\ $$
Commented by mr W last updated on 29/Sep/20
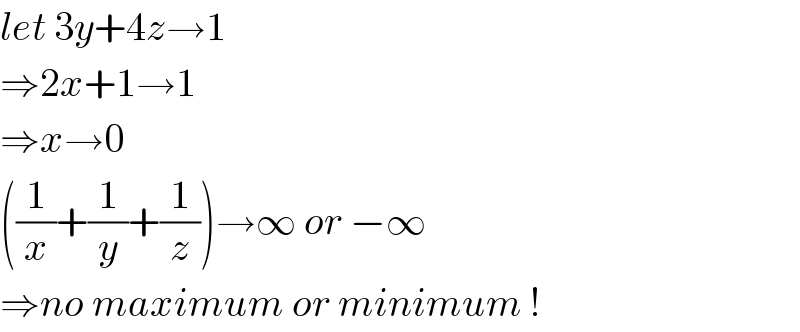
$${let}\:\mathrm{3}{y}+\mathrm{4}{z}\rightarrow\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{x}+\mathrm{1}\rightarrow\mathrm{1} \\ $$$$\Rightarrow{x}\rightarrow\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right)\rightarrow\infty\:{or}\:−\infty \\ $$$$\Rightarrow{no}\:{maximum}\:{or}\:{minimum}\:! \\ $$
