Question Number 98914 by shaxzod last updated on 17/Jun/20
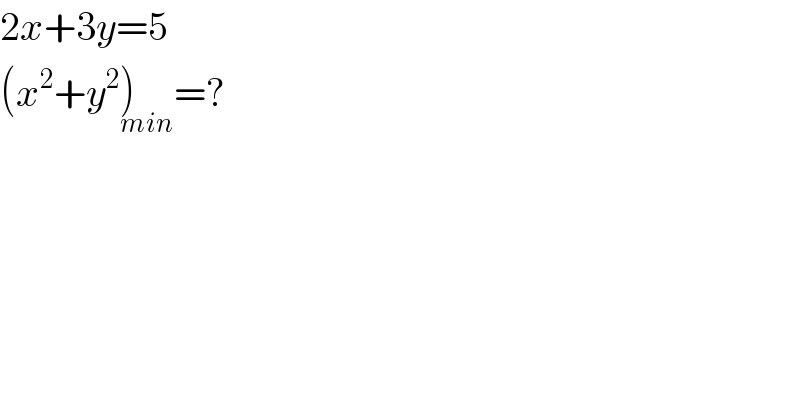
$$\mathrm{2}{x}+\mathrm{3}{y}=\mathrm{5} \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \underset{{min}} {\right)}=? \\ $$
Commented by john santu last updated on 17/Jun/20
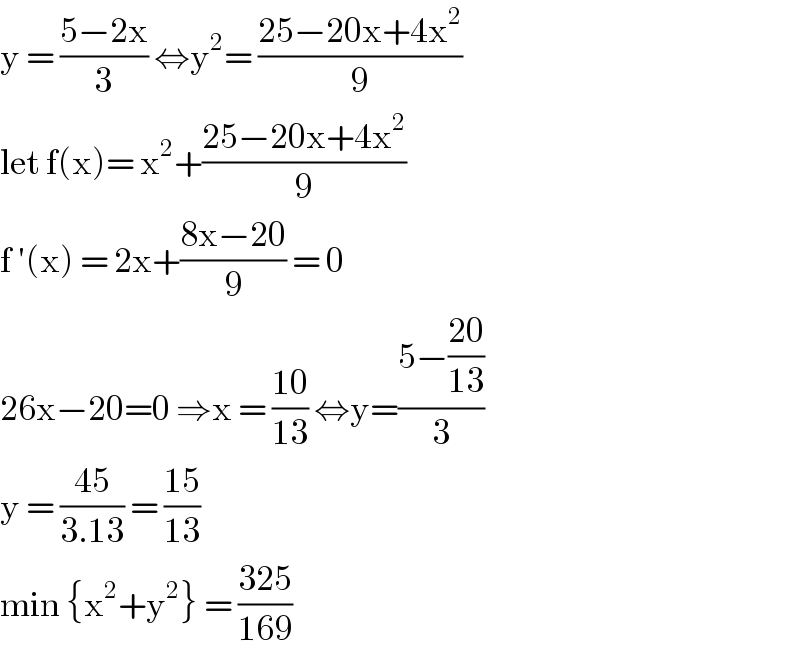
$$\mathrm{y}\:=\:\frac{\mathrm{5}−\mathrm{2x}}{\mathrm{3}}\:\Leftrightarrow\mathrm{y}^{\mathrm{2}} =\:\frac{\mathrm{25}−\mathrm{20x}+\mathrm{4x}^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{25}−\mathrm{20x}+\mathrm{4x}^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)\:=\:\mathrm{2x}+\frac{\mathrm{8x}−\mathrm{20}}{\mathrm{9}}\:=\:\mathrm{0} \\ $$$$\mathrm{26x}−\mathrm{20}=\mathrm{0}\:\Rightarrow\mathrm{x}\:=\:\frac{\mathrm{10}}{\mathrm{13}}\:\Leftrightarrow\mathrm{y}=\frac{\mathrm{5}−\frac{\mathrm{20}}{\mathrm{13}}}{\mathrm{3}} \\ $$$$\mathrm{y}\:=\:\frac{\mathrm{45}}{\mathrm{3}.\mathrm{13}}\:=\:\frac{\mathrm{15}}{\mathrm{13}} \\ $$$$\mathrm{min}\:\left\{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right\}\:=\:\frac{\mathrm{325}}{\mathrm{169}} \\ $$
Commented by mr W last updated on 17/Jun/20

$$\frac{\mathrm{325}}{\mathrm{169}}=\frac{\mathrm{25}}{\mathrm{13}}={correct} \\ $$
Answered by Farruxjano last updated on 17/Jun/20
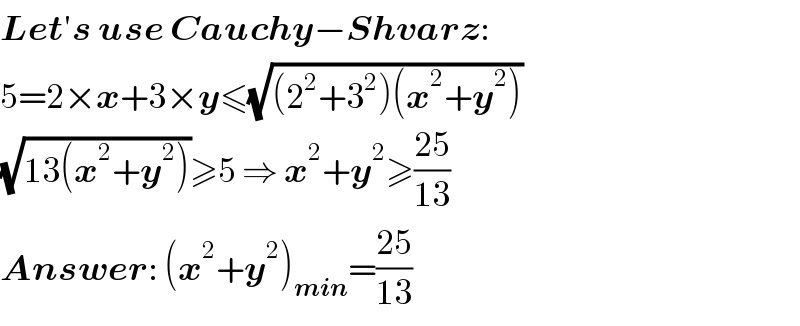
$$\boldsymbol{{Let}}'\boldsymbol{{s}}\:\boldsymbol{{use}}\:\boldsymbol{{Cauchy}}−\boldsymbol{{Shvarz}}: \\ $$$$\mathrm{5}=\mathrm{2}×\boldsymbol{{x}}+\mathrm{3}×\boldsymbol{{y}}\leqslant\sqrt{\left(\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right)\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \right)} \\ $$$$\sqrt{\mathrm{13}\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \right)}\geqslant\mathrm{5}\:\Rightarrow\:\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \geqslant\frac{\mathrm{25}}{\mathrm{13}} \\ $$$$\boldsymbol{{Answer}}:\:\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \right)_{\boldsymbol{{min}}} =\frac{\mathrm{25}}{\mathrm{13}} \\ $$
Commented by john santu last updated on 17/Jun/20
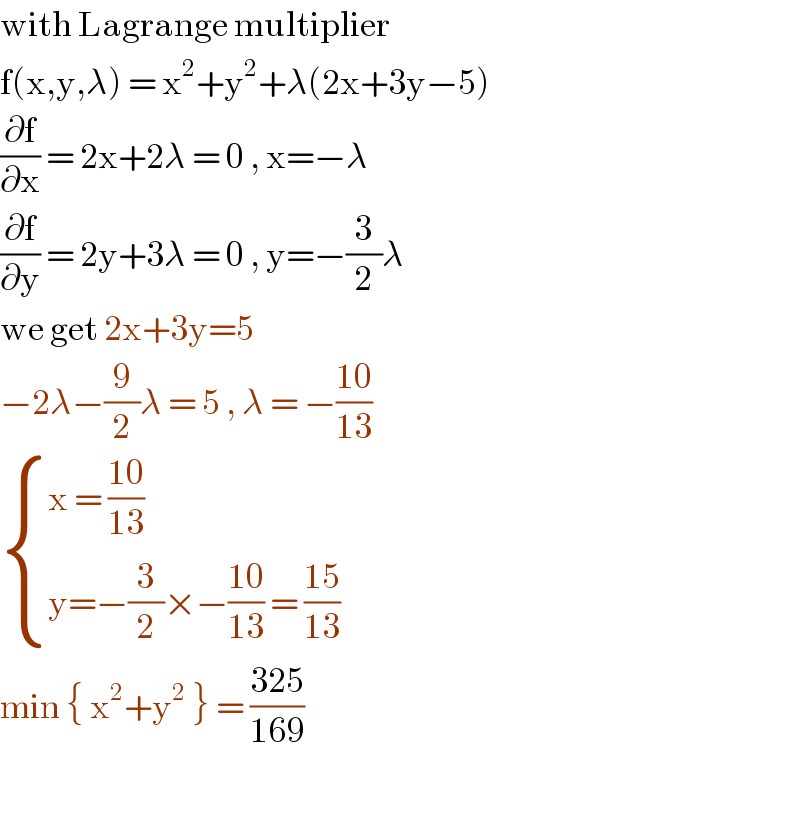
$$\mathrm{with}\:\mathrm{Lagrange}\:\mathrm{multiplier} \\ $$$$\mathrm{f}\left(\mathrm{x},\mathrm{y},\lambda\right)\:=\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\lambda\left(\mathrm{2x}+\mathrm{3y}−\mathrm{5}\right) \\ $$$$\frac{\partial\mathrm{f}}{\partial\mathrm{x}}\:=\:\mathrm{2x}+\mathrm{2}\lambda\:=\:\mathrm{0}\:,\:\mathrm{x}=−\lambda \\ $$$$\frac{\partial\mathrm{f}}{\partial\mathrm{y}}\:=\:\mathrm{2y}+\mathrm{3}\lambda\:=\:\mathrm{0}\:,\:\mathrm{y}=−\frac{\mathrm{3}}{\mathrm{2}}\lambda \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{2x}+\mathrm{3y}=\mathrm{5} \\ $$$$−\mathrm{2}\lambda−\frac{\mathrm{9}}{\mathrm{2}}\lambda\:=\:\mathrm{5}\:,\:\lambda\:=\:−\frac{\mathrm{10}}{\mathrm{13}} \\ $$$$\begin{cases}{\mathrm{x}\:=\:\frac{\mathrm{10}}{\mathrm{13}}}\\{\mathrm{y}=−\frac{\mathrm{3}}{\mathrm{2}}×−\frac{\mathrm{10}}{\mathrm{13}}\:=\:\frac{\mathrm{15}}{\mathrm{13}}}\end{cases} \\ $$$$\mathrm{min}\:\left\{\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:\right\}\:=\:\frac{\mathrm{325}}{\mathrm{169}} \\ $$$$ \\ $$
Answered by maths mind last updated on 17/Jun/20
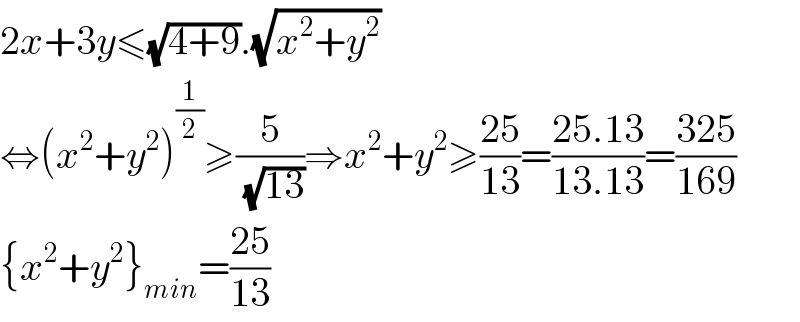
$$\mathrm{2}{x}+\mathrm{3}{y}\leqslant\sqrt{\mathrm{4}+\mathrm{9}}.\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \geqslant\frac{\mathrm{5}}{\:\sqrt{\mathrm{13}}}\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \geqslant\frac{\mathrm{25}}{\mathrm{13}}=\frac{\mathrm{25}.\mathrm{13}}{\mathrm{13}.\mathrm{13}}=\frac{\mathrm{325}}{\mathrm{169}} \\ $$$$\left\{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}_{{min}} =\frac{\mathrm{25}}{\mathrm{13}} \\ $$
Answered by mr W last updated on 17/Jun/20
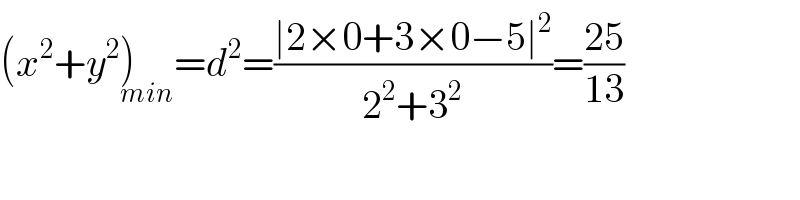
$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \underset{{min}} {\right)}={d}^{\mathrm{2}} =\frac{\mid\mathrm{2}×\mathrm{0}+\mathrm{3}×\mathrm{0}−\mathrm{5}\mid^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\frac{\mathrm{25}}{\mathrm{13}} \\ $$
