Question Number 162240 by Gbenga last updated on 27/Dec/21

$$\int\frac{\mathrm{2}\boldsymbol{{x}}−\mathrm{5}}{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{{x}}+\mathrm{5}}\boldsymbol{{dx}} \\ $$
Answered by Ar Brandon last updated on 27/Dec/21
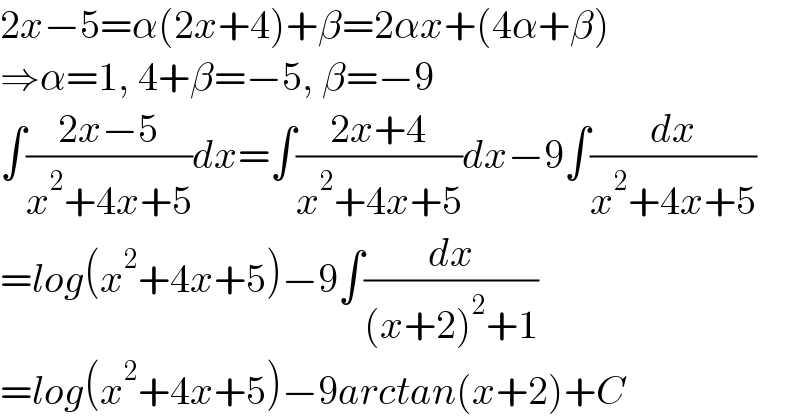
$$\mathrm{2}{x}−\mathrm{5}=\alpha\left(\mathrm{2}{x}+\mathrm{4}\right)+\beta=\mathrm{2}\alpha{x}+\left(\mathrm{4}\alpha+\beta\right) \\ $$$$\Rightarrow\alpha=\mathrm{1},\:\mathrm{4}+\beta=−\mathrm{5},\:\beta=−\mathrm{9} \\ $$$$\int\frac{\mathrm{2}{x}−\mathrm{5}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}{dx}=\int\frac{\mathrm{2}{x}+\mathrm{4}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}{dx}−\mathrm{9}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}} \\ $$$$={log}\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}\right)−\mathrm{9}\int\frac{{dx}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$={log}\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}\right)−\mathrm{9}{arctan}\left({x}+\mathrm{2}\right)+{C} \\ $$
