Question Number 19729 by Joel577 last updated on 15/Aug/17
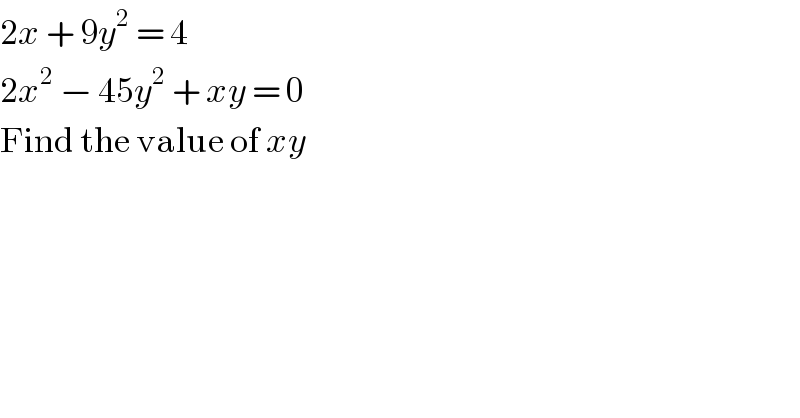
$$\mathrm{2}{x}\:+\:\mathrm{9}{y}^{\mathrm{2}} \:=\:\mathrm{4} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} \:−\:\mathrm{45}{y}^{\mathrm{2}} \:+\:{xy}\:=\:\mathrm{0} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{xy} \\ $$
Answered by mrW1 last updated on 15/Aug/17
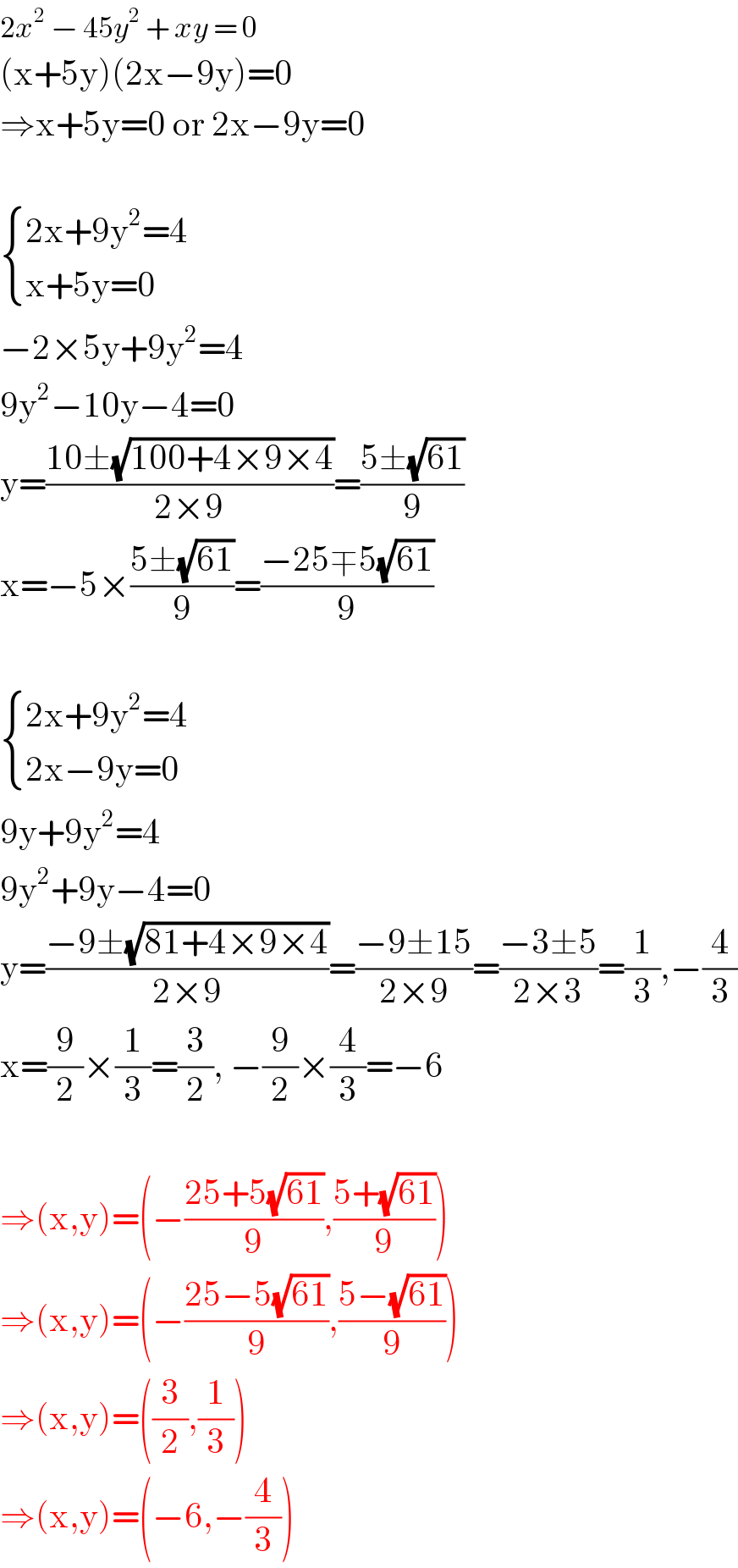
$$\mathrm{2}{x}^{\mathrm{2}} \:−\:\mathrm{45}{y}^{\mathrm{2}} \:+\:{xy}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{5y}\right)\left(\mathrm{2x}−\mathrm{9y}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}+\mathrm{5y}=\mathrm{0}\:\mathrm{or}\:\mathrm{2x}−\mathrm{9y}=\mathrm{0} \\ $$$$ \\ $$$$\begin{cases}{\mathrm{2x}+\mathrm{9y}^{\mathrm{2}} =\mathrm{4}}\\{\mathrm{x}+\mathrm{5y}=\mathrm{0}}\end{cases} \\ $$$$−\mathrm{2}×\mathrm{5y}+\mathrm{9y}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{9y}^{\mathrm{2}} −\mathrm{10y}−\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{y}=\frac{\mathrm{10}\pm\sqrt{\mathrm{100}+\mathrm{4}×\mathrm{9}×\mathrm{4}}}{\mathrm{2}×\mathrm{9}}=\frac{\mathrm{5}\pm\sqrt{\mathrm{61}}}{\mathrm{9}} \\ $$$$\mathrm{x}=−\mathrm{5}×\frac{\mathrm{5}\pm\sqrt{\mathrm{61}}}{\mathrm{9}}=\frac{−\mathrm{25}\mp\mathrm{5}\sqrt{\mathrm{61}}}{\mathrm{9}} \\ $$$$ \\ $$$$\begin{cases}{\mathrm{2x}+\mathrm{9y}^{\mathrm{2}} =\mathrm{4}}\\{\mathrm{2x}−\mathrm{9y}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{9y}+\mathrm{9y}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{9y}^{\mathrm{2}} +\mathrm{9y}−\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{y}=\frac{−\mathrm{9}\pm\sqrt{\mathrm{81}+\mathrm{4}×\mathrm{9}×\mathrm{4}}}{\mathrm{2}×\mathrm{9}}=\frac{−\mathrm{9}\pm\mathrm{15}}{\mathrm{2}×\mathrm{9}}=\frac{−\mathrm{3}\pm\mathrm{5}}{\mathrm{2}×\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}},−\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{x}=\frac{\mathrm{9}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{3}}{\mathrm{2}},\:−\frac{\mathrm{9}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{3}}=−\mathrm{6} \\ $$$$ \\ $$$$\Rightarrow\left(\mathrm{x},\mathrm{y}\right)=\left(−\frac{\mathrm{25}+\mathrm{5}\sqrt{\mathrm{61}}}{\mathrm{9}},\frac{\mathrm{5}+\sqrt{\mathrm{61}}}{\mathrm{9}}\right) \\ $$$$\Rightarrow\left(\mathrm{x},\mathrm{y}\right)=\left(−\frac{\mathrm{25}−\mathrm{5}\sqrt{\mathrm{61}}}{\mathrm{9}},\frac{\mathrm{5}−\sqrt{\mathrm{61}}}{\mathrm{9}}\right) \\ $$$$\Rightarrow\left(\mathrm{x},\mathrm{y}\right)=\left(\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\Rightarrow\left(\mathrm{x},\mathrm{y}\right)=\left(−\mathrm{6},−\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$
