Menu Close

2xy-cos-y-dx-x-2-xsiny-2y-dy-0-

Tinku Tara 0 Comments
Pin




Question Number 105710 by john santu last updated on 31/Jul/20
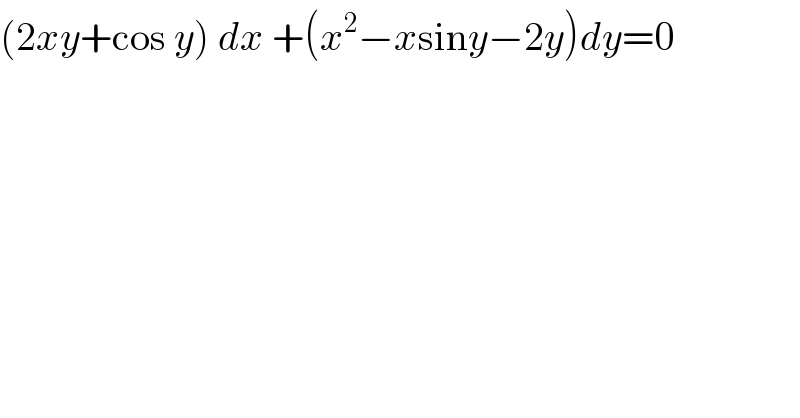
(2xy+cos y) dx +(x^2 −xsiny−2y)dy=0
$$\left(\mathrm{2}{xy}+\mathrm{cos}\:{y}\right)\:{dx}\:+\left({x}^{\mathrm{2}} −{x}\mathrm{sin}{y}−\mathrm{2}{y}\right){dy}=\mathrm{0} \\ $$
Answered by Smail last updated on 31/Jul/20
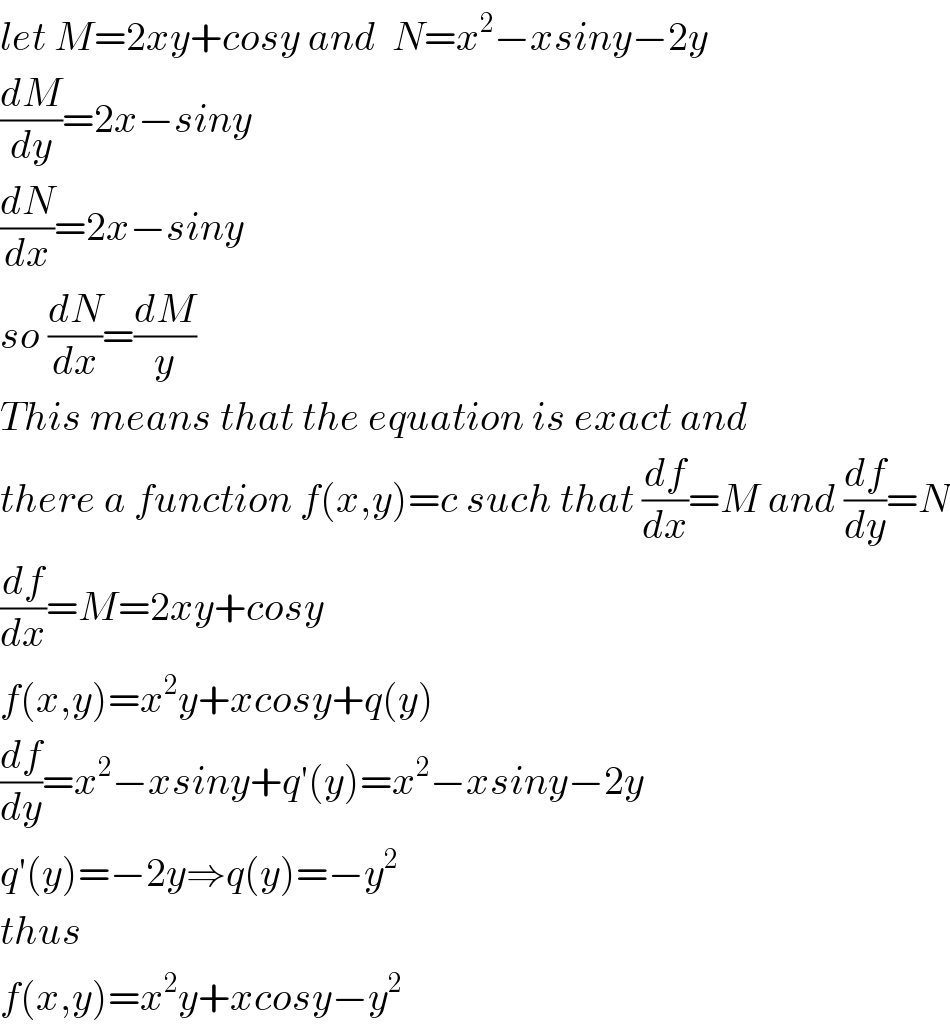
let M=2xy+cosy and N=x^2 −xsiny−2y (dM/dy)=2x−siny (dN/dx)=2x−siny so (dN/dx)=(dM/y) This means that the equation is exact and there a function f(x,y)=c such that (df/dx)=M and (df/dy)=N (df/dx)=M=2xy+cosy f(x,y)=x^2 y+xcosy+q(y) (df/dy)=x^2 −xsiny+q′(y)=x^2 −xsiny−2y q′(y)=−2y⇒q(y)=−y^2 thus f(x,y)=x^2 y+xcosy−y^2
$${let}\:{M}=\mathrm{2}{xy}+{cosy}\:{and}\:\:{N}={x}^{\mathrm{2}} −{xsiny}−\mathrm{2}{y} \\ $$$$\frac{{dM}}{{dy}}=\mathrm{2}{x}−{siny} \\ $$$$\frac{{dN}}{{dx}}=\mathrm{2}{x}−{siny} \\ $$$${so}\:\frac{{dN}}{{dx}}=\frac{{dM}}{{y}} \\ $$$${This}\:{means}\:{that}\:{the}\:{equation}\:{is}\:{exact}\:{and} \\ $$$${there}\:{a}\:{function}\:{f}\left({x},{y}\right)={c}\:{such}\:{that}\:\frac{{df}}{{dx}}={M}\:{and}\:\frac{{df}}{{dy}}={N} \\ $$$$\frac{{df}}{{dx}}={M}=\mathrm{2}{xy}+{cosy} \\ $$$${f}\left({x},{y}\right)={x}^{\mathrm{2}} {y}+{xcosy}+{q}\left({y}\right) \\ $$$$\frac{{df}}{{dy}}={x}^{\mathrm{2}} −{xsiny}+{q}'\left({y}\right)={x}^{\mathrm{2}} −{xsiny}−\mathrm{2}{y} \\ $$$${q}'\left({y}\right)=−\mathrm{2}{y}\Rightarrow{q}\left({y}\right)=−{y}^{\mathrm{2}} \\ $$$${thus} \\ $$$${f}\left({x},{y}\right)={x}^{\mathrm{2}} {y}+{xcosy}−{y}^{\mathrm{2}} \\ $$
Answered by bobhans last updated on 31/Jul/20
(∂M/∂y) = 2x−sin y ; (∂N/∂x) = 2x−sin y ⇔ (∂M/∂y) = (∂N/∂x) ⇔ exact diff equation F(x,y)= ∫ (2xy+cos y) dx + g(y) F(x,y)= x^2 y+xcos y + g(y) g ′(y)= (x^2 −xsin y−2y)−(∂/∂y)[ x^2 y+xcos y ] g(y) = ∫ (x^2 −xsin y−2y−(x^2 −xsin y))dy g(y) = ∫(−2y)dy = −y^2 Solution x^2 y + xcos y−y^2 = C ★
$$\frac{\partial{M}}{\partial{y}}\:=\:\mathrm{2}{x}−\mathrm{sin}\:{y}\:;\:\frac{\partial{N}}{\partial{x}}\:=\:\mathrm{2}{x}−\mathrm{sin}\:{y} \\ $$$$\Leftrightarrow\:\frac{\partial{M}}{\partial{y}}\:=\:\frac{\partial{N}}{\partial{x}}\:\Leftrightarrow\:{exact}\:{diff}\:{equation} \\ $$$${F}\left({x},{y}\right)=\:\int\:\left(\mathrm{2}{xy}+\mathrm{cos}\:{y}\right)\:{dx}\:+\:{g}\left({y}\right) \\ $$$${F}\left({x},{y}\right)=\:{x}^{\mathrm{2}} {y}+{x}\mathrm{cos}\:{y}\:+\:{g}\left({y}\right) \\ $$$${g}\:'\left({y}\right)=\:\left({x}^{\mathrm{2}} −{x}\mathrm{sin}\:{y}−\mathrm{2}{y}\right)−\frac{\partial}{\partial{y}}\left[\:{x}^{\mathrm{2}} {y}+{x}\mathrm{cos}\:{y}\:\right] \\ $$$${g}\left({y}\right)\:=\:\int\:\left({x}^{\mathrm{2}} −{x}\mathrm{sin}\:{y}−\mathrm{2}{y}−\left({x}^{\mathrm{2}} −{x}\mathrm{sin}\:{y}\right)\right){dy} \\ $$$${g}\left({y}\right)\:=\:\int\left(−\mathrm{2}{y}\right){dy}\:=\:−{y}^{\mathrm{2}} \\ $$$$\mathcal{S}{olution}\: \\ $$$${x}^{\mathrm{2}} {y}\:+\:{x}\mathrm{cos}\:{y}−{y}^{\mathrm{2}} \:=\:{C}\:\bigstar \\ $$
Answered by 1549442205PVT last updated on 31/Jul/20
This is an full differential equation since P(x,y)=2xy+cosy,Q(x,y)=x^2 −xsiny−2y and (∂P/∂y)=(∂Q/∂x)=2x−siny We find general integration byformular ∫_x_0 ^x P(x,y)dx+∫_y_0 ^( y) Q(x,y)dy=C Take x_0 =0,y_0 =0,we obtain: ∫_0 ^( x) (2xy+cosy)dx+∫_0 ^( y) (x^2 −xsiny−2y)dy ⇔(x^2 y+xcosy)∣_0 ^x +(x^2 y+xcosy−y^2 )∣_0 ^y =C_1 ⇔x^2 y+xcosy+x^2 y+xcosy−y^2 −x=C_1 ⇔2(x^2 y+xcosy)−x−y^2 =C
$$\mathrm{This}\:\mathrm{is}\:\mathrm{an}\:\mathrm{full}\:\mathrm{differential}\:\mathrm{equation} \\ $$$$\mathrm{since}\:\mathrm{P}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{2xy}+\mathrm{cosy},\mathrm{Q}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{xsiny}−\mathrm{2y} \\ $$$$\mathrm{and}\:\frac{\partial\mathrm{P}}{\partial\mathrm{y}}=\frac{\partial\mathrm{Q}}{\partial\mathrm{x}}=\mathrm{2x}−\mathrm{siny} \\ $$$$\mathrm{We}\:\mathrm{find}\:\mathrm{general}\:\mathrm{integration}\:\mathrm{byformular} \\ $$$$\int_{\mathrm{x}_{\mathrm{0}} } ^{\mathrm{x}} \mathrm{P}\left(\mathrm{x},\mathrm{y}\right)\mathrm{dx}+\int_{\mathrm{y}_{\mathrm{0}} } ^{\:\mathrm{y}} \mathrm{Q}\left(\mathrm{x},\mathrm{y}\right)\mathrm{dy}=\mathrm{C} \\ $$$$\mathrm{Take}\:\mathrm{x}_{\mathrm{0}} =\mathrm{0},\mathrm{y}_{\mathrm{0}} =\mathrm{0},\mathrm{we}\:\mathrm{obtain}: \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{x}} \left(\mathrm{2xy}+\mathrm{cosy}\right)\mathrm{dx}+\int_{\mathrm{0}} ^{\:\mathrm{y}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{xsiny}−\mathrm{2y}\right)\mathrm{dy} \\ $$$$\Leftrightarrow\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{xcosy}\right)\mid_{\mathrm{0}} ^{\mathrm{x}} +\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{xcosy}−\mathrm{y}^{\mathrm{2}} \right)\mid_{\mathrm{0}} ^{\mathrm{y}} =\mathrm{C}_{\mathrm{1}} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{xcosy}+\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{xcosy}−\mathrm{y}^{\mathrm{2}} −\mathrm{x}=\mathrm{C}_{\mathrm{1}} \\ $$$$\Leftrightarrow\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{xcosy}\right)−\mathrm{x}−\mathrm{y}^{\mathrm{2}} =\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *