Question Number 104592 by bemath last updated on 22/Jul/20
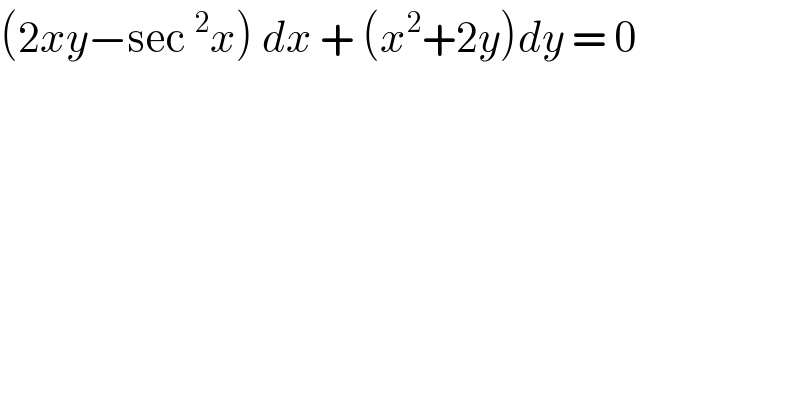
$$\left(\mathrm{2}{xy}−\mathrm{sec}\:^{\mathrm{2}} {x}\right)\:{dx}\:+\:\left({x}^{\mathrm{2}} +\mathrm{2}{y}\right){dy}\:=\:\mathrm{0} \\ $$
Answered by john santu last updated on 28/Jul/20
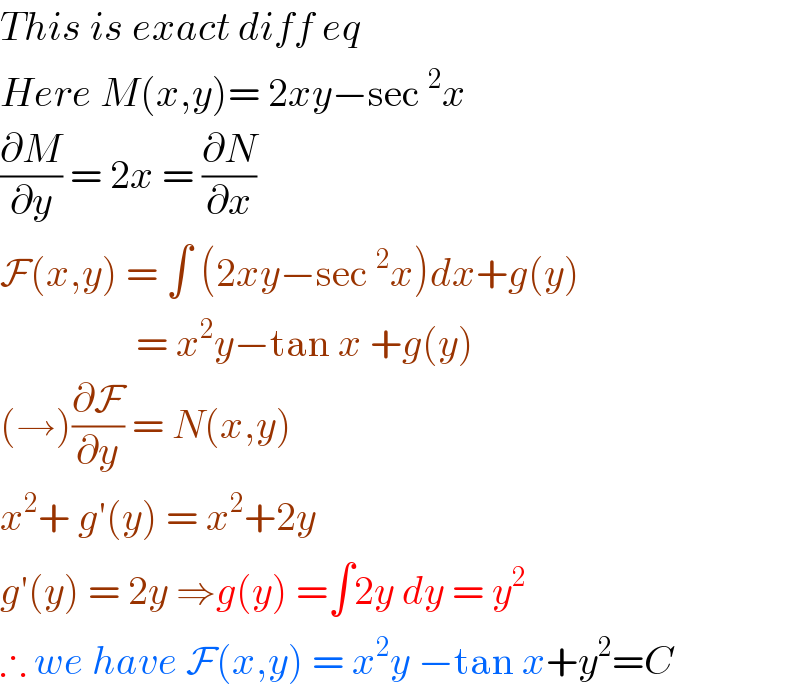
$${This}\:{is}\:{exact}\:{diff}\:{eq}\: \\ $$$${Here}\:{M}\left({x},{y}\right)=\:\mathrm{2}{xy}−\mathrm{sec}\:^{\mathrm{2}} {x}\: \\ $$$$\frac{\partial{M}}{\partial{y}}\:=\:\mathrm{2}{x}\:=\:\frac{\partial{N}}{\partial{x}}\: \\ $$$$\mathcal{F}\left({x},{y}\right)\:=\:\int\:\left(\mathrm{2}{xy}−\mathrm{sec}\:^{\mathrm{2}} {x}\right){dx}+{g}\left({y}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{x}^{\mathrm{2}} {y}−\mathrm{tan}\:{x}\:+{g}\left({y}\right) \\ $$$$\left(\rightarrow\right)\frac{\partial\mathcal{F}}{\partial{y}}\:=\:{N}\left({x},{y}\right) \\ $$$${x}^{\mathrm{2}} +\:{g}'\left({y}\right)\:=\:{x}^{\mathrm{2}} +\mathrm{2}{y}\: \\ $$$${g}'\left({y}\right)\:=\:\mathrm{2}{y}\:\Rightarrow{g}\left({y}\right)\:=\int\mathrm{2}{y}\:{dy}\:=\:{y}^{\mathrm{2}} \\ $$$$\therefore\:{we}\:{have}\:\mathcal{F}\left({x},{y}\right)\:=\:{x}^{\mathrm{2}} {y}\:−\mathrm{tan}\:{x}+{y}^{\mathrm{2}} ={C} \\ $$
