Question Number 122163 by benjo_mathlover last updated on 14/Nov/20
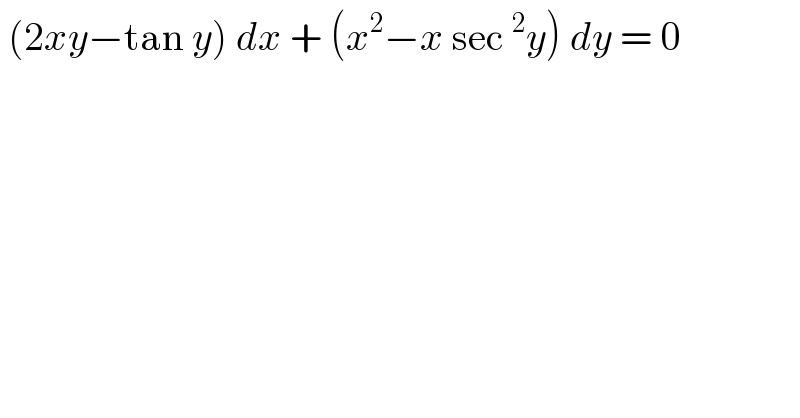
$$\:\left(\mathrm{2}{xy}−\mathrm{tan}\:{y}\right)\:{dx}\:+\:\left({x}^{\mathrm{2}} −{x}\:\mathrm{sec}\:^{\mathrm{2}} {y}\right)\:{dy}\:=\:\mathrm{0}\: \\ $$
Answered by liberty last updated on 14/Nov/20
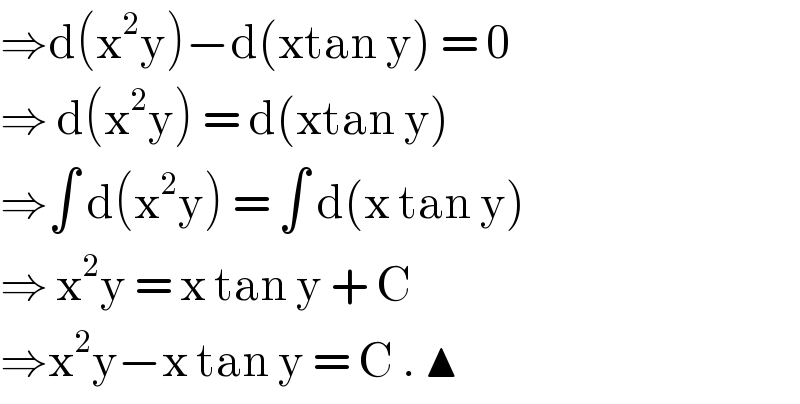
$$\Rightarrow\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}\right)−\mathrm{d}\left(\mathrm{xtan}\:\mathrm{y}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}\right)\:=\:\mathrm{d}\left(\mathrm{xtan}\:\mathrm{y}\right)\: \\ $$$$\Rightarrow\int\:\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}\right)\:=\:\int\:\mathrm{d}\left(\mathrm{x}\:\mathrm{tan}\:\mathrm{y}\right) \\ $$$$\Rightarrow\:\mathrm{x}^{\mathrm{2}} \mathrm{y}\:=\:\mathrm{x}\:\mathrm{tan}\:\mathrm{y}\:+\:\mathrm{C} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} \mathrm{y}−\mathrm{x}\:\mathrm{tan}\:\mathrm{y}\:=\:\mathrm{C}\:.\:\blacktriangle\: \\ $$
