Question Number 85834 by sahnaz last updated on 25/Mar/20
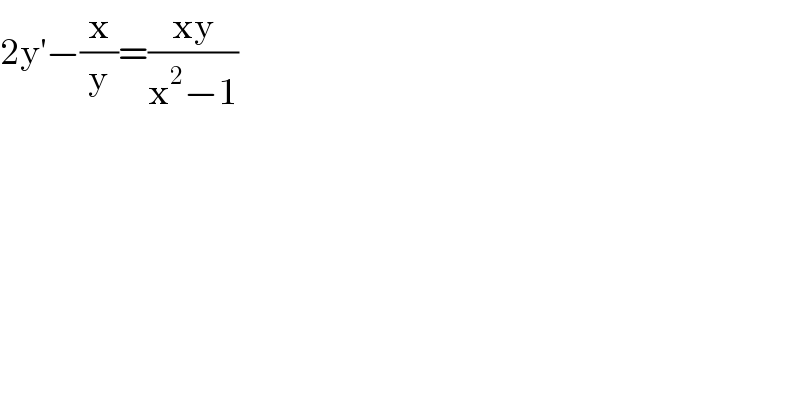
$$\mathrm{2y}^{'} −\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{xy}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}} \\ $$
Answered by mind is power last updated on 27/Mar/20
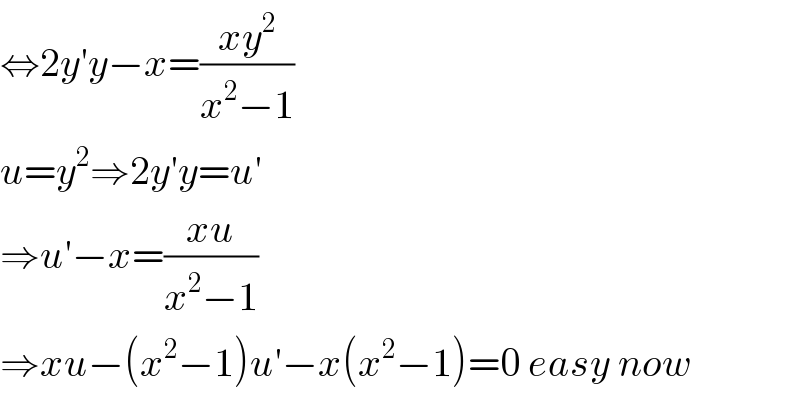
$$\Leftrightarrow\mathrm{2}{y}'{y}−{x}=\frac{{xy}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$${u}={y}^{\mathrm{2}} \Rightarrow\mathrm{2}{y}'{y}={u}' \\ $$$$\Rightarrow{u}'−{x}=\frac{{xu}}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow{xu}−\left({x}^{\mathrm{2}} −\mathrm{1}\right){u}'−{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0}\:{easy}\:{now} \\ $$
