Question Number 95801 by bobhans last updated on 27/May/20
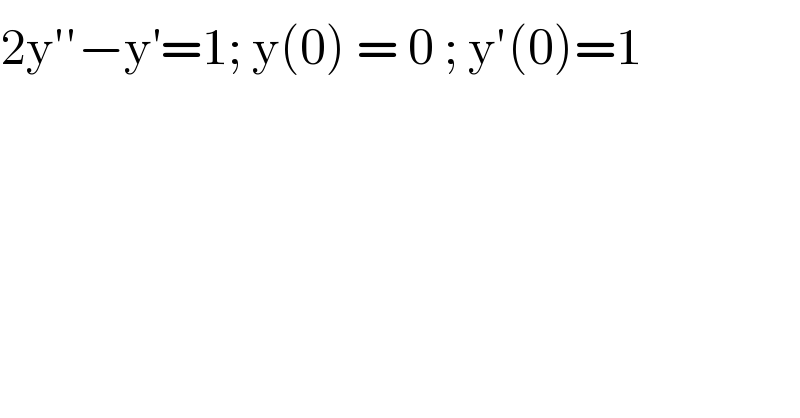
$$\mathrm{2y}''−\mathrm{y}^{'} =\mathrm{1};\:\mathrm{y}\left(\mathrm{0}\right)\:=\:\mathrm{0}\:;\:\mathrm{y}'\left(\mathrm{0}\right)=\mathrm{1} \\ $$
Answered by mr W last updated on 27/May/20
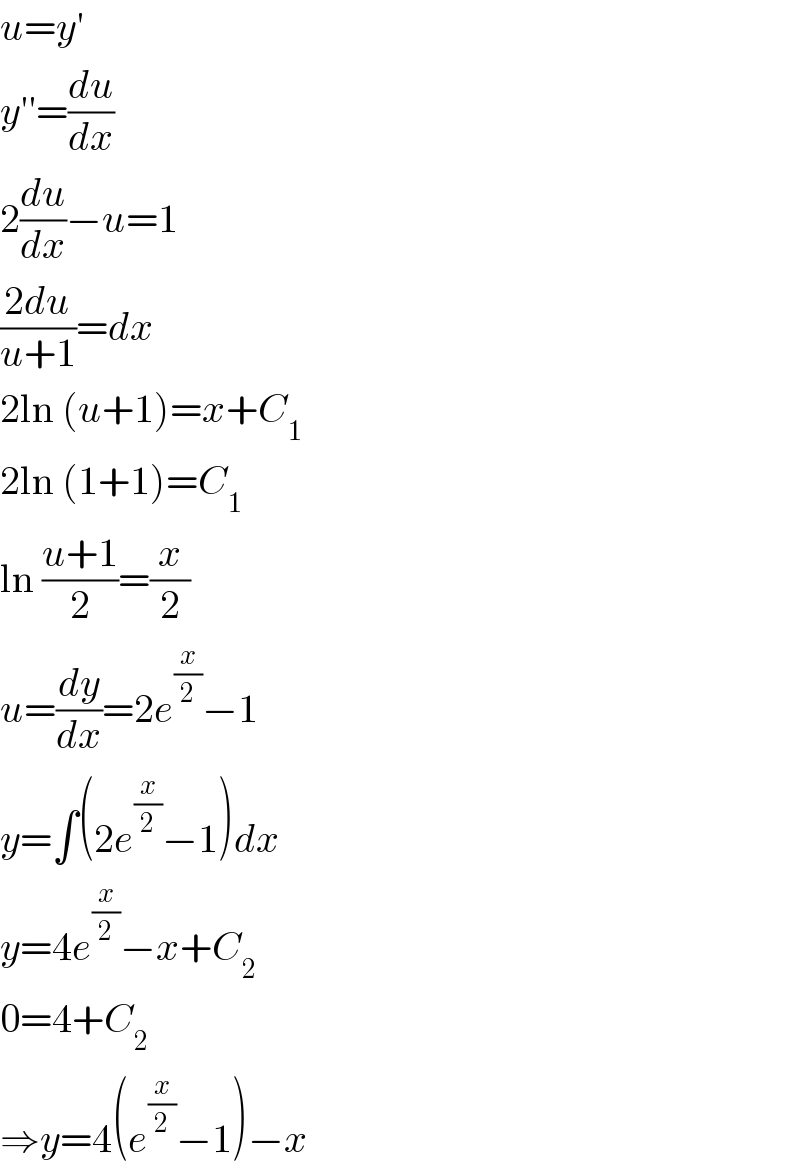
$${u}={y}' \\ $$$${y}''=\frac{{du}}{{dx}} \\ $$$$\mathrm{2}\frac{{du}}{{dx}}−{u}=\mathrm{1} \\ $$$$\frac{\mathrm{2}{du}}{{u}+\mathrm{1}}={dx} \\ $$$$\mathrm{2ln}\:\left({u}+\mathrm{1}\right)={x}+{C}_{\mathrm{1}} \\ $$$$\mathrm{2ln}\:\left(\mathrm{1}+\mathrm{1}\right)={C}_{\mathrm{1}} \\ $$$$\mathrm{ln}\:\frac{{u}+\mathrm{1}}{\mathrm{2}}=\frac{{x}}{\mathrm{2}} \\ $$$${u}=\frac{{dy}}{{dx}}=\mathrm{2}{e}^{\frac{{x}}{\mathrm{2}}} −\mathrm{1} \\ $$$${y}=\int\left(\mathrm{2}{e}^{\frac{{x}}{\mathrm{2}}} −\mathrm{1}\right){dx} \\ $$$${y}=\mathrm{4}{e}^{\frac{{x}}{\mathrm{2}}} −{x}+{C}_{\mathrm{2}} \\ $$$$\mathrm{0}=\mathrm{4}+{C}_{\mathrm{2}} \\ $$$$\Rightarrow{y}=\mathrm{4}\left({e}^{\frac{{x}}{\mathrm{2}}} −\mathrm{1}\right)−{x} \\ $$
Answered by john santu last updated on 28/May/20
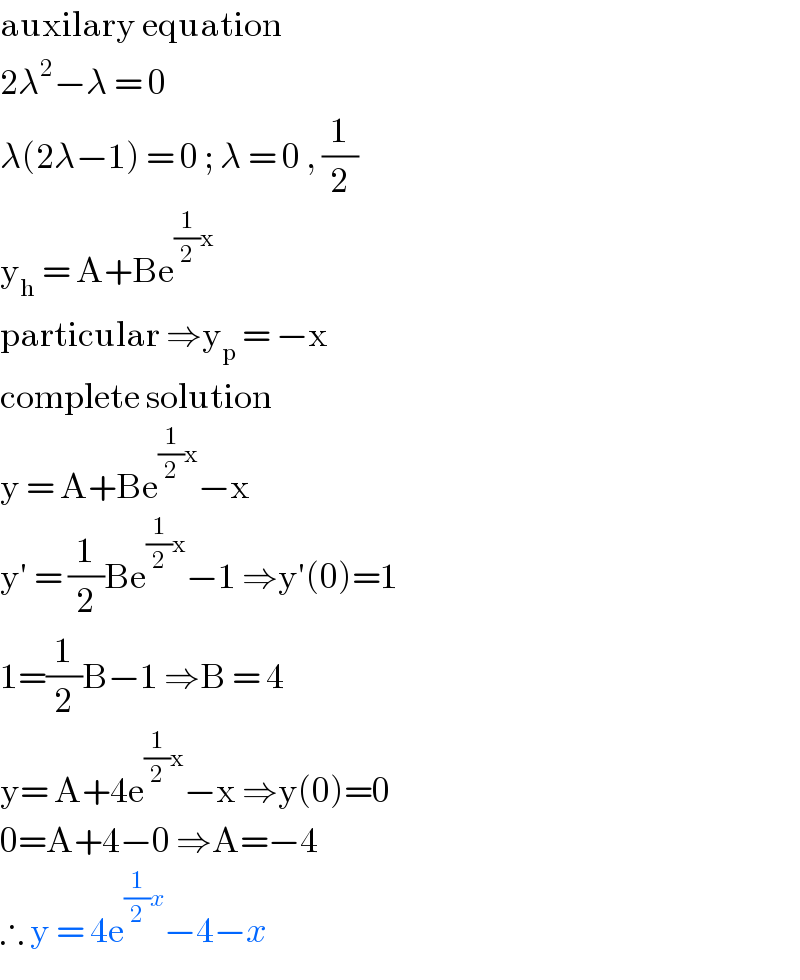
$$\mathrm{auxilary}\:\mathrm{equation} \\ $$$$\mathrm{2}\lambda^{\mathrm{2}} −\lambda\:=\:\mathrm{0} \\ $$$$\lambda\left(\mathrm{2}\lambda−\mathrm{1}\right)\:=\:\mathrm{0}\:;\:\lambda\:=\:\mathrm{0}\:,\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{A}+\mathrm{Be}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}} \: \\ $$$$\mathrm{particular}\:\Rightarrow\mathrm{y}_{\mathrm{p}} \:=\:−\mathrm{x}\: \\ $$$$\mathrm{complete}\:\mathrm{solution}\: \\ $$$$\mathrm{y}\:=\:\mathrm{A}+\mathrm{Be}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}} −\mathrm{x}\: \\ $$$$\mathrm{y}'\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Be}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}} −\mathrm{1}\:\Rightarrow\mathrm{y}'\left(\mathrm{0}\right)=\mathrm{1}\: \\ $$$$\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{B}−\mathrm{1}\:\Rightarrow\mathrm{B}\:=\:\mathrm{4}\: \\ $$$$\mathrm{y}=\:\mathrm{A}+\mathrm{4e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}} −\mathrm{x}\:\Rightarrow\mathrm{y}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{0}=\mathrm{A}+\mathrm{4}−\mathrm{0}\:\Rightarrow\mathrm{A}=−\mathrm{4}\: \\ $$$$\therefore\:\mathrm{y}\:=\:\mathrm{4e}^{\frac{\mathrm{1}}{\mathrm{2}}{x}} −\mathrm{4}−{x}\: \\ $$
