Menu Close

2yz-4z-2x-2-0-2xz-2z-2y-4-0-2xy-4x-2y-2z-4-0-how-to-find-the-all-values-of-the-x-y-z-

Tinku Tara 0 Comments
Pin




Question Number 184258 by universe last updated on 04/Jan/23
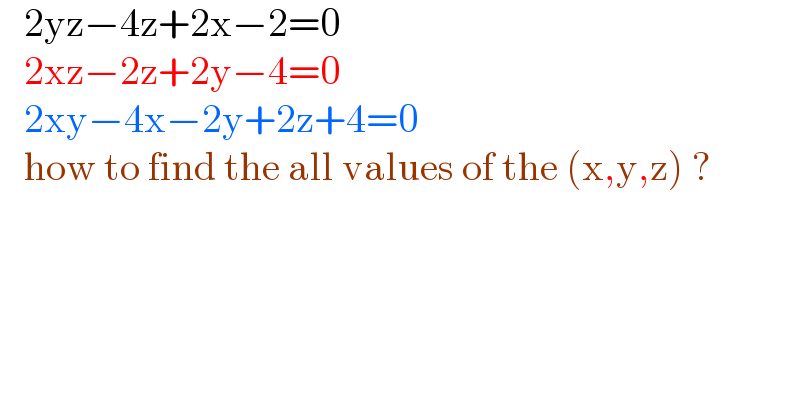
2yz−4z+2x−2=0 2xz−2z+2y−4=0 2xy−4x−2y+2z+4=0 how to find the all values of the (x,y,z) ?
$$\:\:\:\mathrm{2yz}−\mathrm{4z}+\mathrm{2x}−\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\mathrm{2xz}−\mathrm{2z}+\mathrm{2y}−\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\mathrm{2xy}−\mathrm{4x}−\mathrm{2y}+\mathrm{2z}+\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\mathrm{how}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{all}\:\mathrm{values}\:\mathrm{of}\:\mathrm{the}\:\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)\:? \\ $$
Answered by SEKRET last updated on 04/Jan/23
(0,1,−1) (0,3,1) (1,2,0)(2,1,1)(2,3,−1)
$$\:\left(\mathrm{0},\mathrm{1},−\mathrm{1}\right)\:\left(\mathrm{0},\mathrm{3},\mathrm{1}\right)\:\left(\mathrm{1},\mathrm{2},\mathrm{0}\right)\left(\mathrm{2},\mathrm{1},\mathrm{1}\right)\left(\mathrm{2},\mathrm{3},−\mathrm{1}\right) \\ $$
Answered by SEKRET last updated on 04/Jan/23
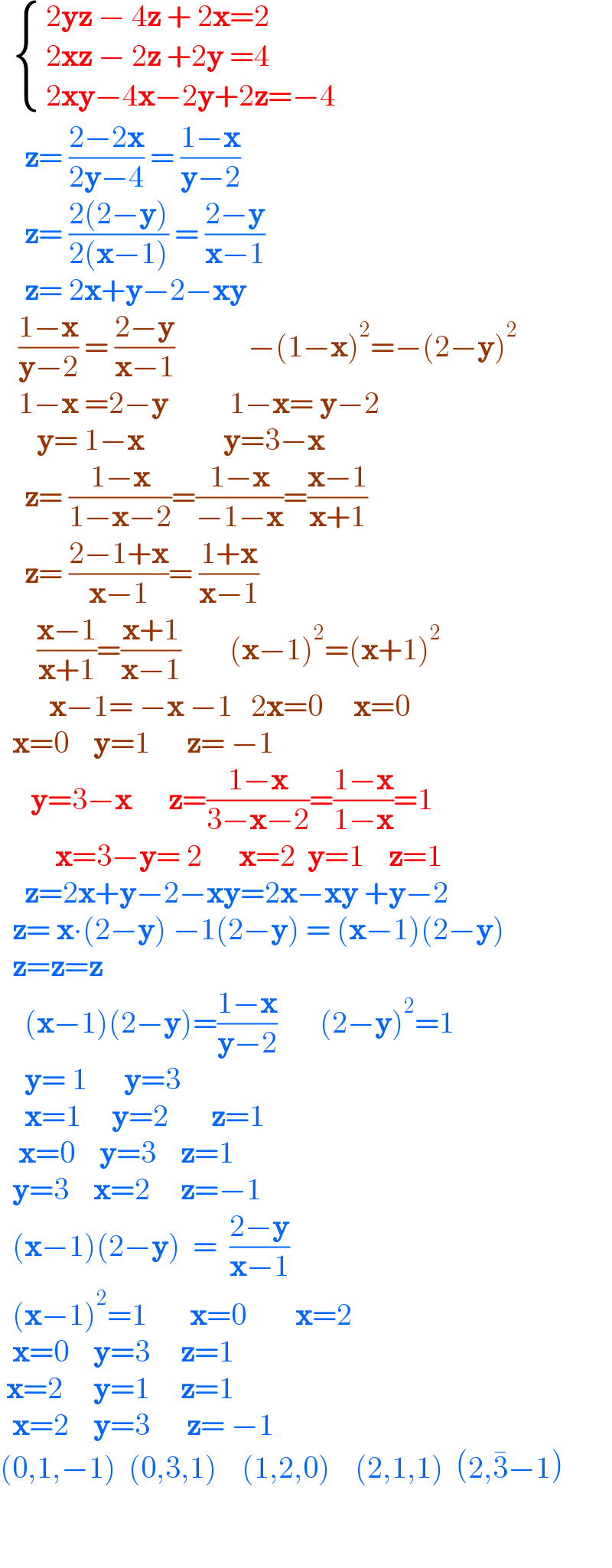
{ (( 2yz − 4z + 2x=2)),(( 2xz − 2z +2y =4)),(( 2xy−4x−2y+2z=−4)) :} z= ((2−2x)/(2y−4)) = ((1−x)/(y−2)) z= ((2(2−y))/(2(x−1))) = ((2−y)/(x−1)) z= 2x+y−2−xy ((1−x)/(y−2)) = ((2−y)/(x−1)) −(1−x)^2 =−(2−y)^2 1−x =2−y 1−x= y−2 y= 1−x y=3−x z= ((1−x)/(1−x−2))=((1−x)/(−1−x))=((x−1)/(x+1)) z= ((2−1+x)/(x−1))= ((1+x)/(x−1)) ((x−1)/(x+1))=((x+1)/(x−1)) (x−1)^2 =(x+1)^2 x−1= −x −1 2x=0 x=0 x=0 y=1 z= −1 y=3−x z=((1−x)/(3−x−2))=((1−x)/(1−x))=1 x=3−y= 2 x=2 y=1 z=1 z=2x+y−2−xy=2x−xy +y−2 z= x∙(2−y) −1(2−y) = (x−1)(2−y) z=z=z (x−1)(2−y)=((1−x)/(y−2)) (2−y)^2 =1 y= 1 y=3 x=1 y=2 z=1 x=0 y=3 z=1 y=3 x=2 z=−1 (x−1)(2−y) = ((2−y)/(x−1)) (x−1)^2 =1 x=0 x=2 x=0 y=3 z=1 x=2 y=1 z=1 x=2 y=3 z= −1 (0,1,−1) (0,3,1) (1,2,0) (2,1,1) (2,3^� −1)
$$\:\:\begin{cases}{\:\mathrm{2}\boldsymbol{\mathrm{yz}}\:−\:\mathrm{4}\boldsymbol{\mathrm{z}}\:+\:\mathrm{2}\boldsymbol{\mathrm{x}}=\mathrm{2}}\\{\:\mathrm{2}\boldsymbol{\mathrm{xz}}\:−\:\mathrm{2}\boldsymbol{\mathrm{z}}\:+\mathrm{2}\boldsymbol{\mathrm{y}}\:=\mathrm{4}}\\{\:\mathrm{2}\boldsymbol{\mathrm{xy}}−\mathrm{4}\boldsymbol{\mathrm{x}}−\mathrm{2}\boldsymbol{\mathrm{y}}+\mathrm{2}\boldsymbol{\mathrm{z}}=−\mathrm{4}}\end{cases} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{z}}=\:\frac{\mathrm{2}−\mathrm{2}\boldsymbol{\mathrm{x}}}{\mathrm{2}\boldsymbol{\mathrm{y}}−\mathrm{4}}\:=\:\frac{\mathrm{1}−\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{y}}−\mathrm{2}} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{z}}=\:\frac{\mathrm{2}\left(\mathrm{2}−\boldsymbol{\mathrm{y}}\right)}{\mathrm{2}\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)}\:=\:\frac{\mathrm{2}−\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{x}}−\mathrm{1}} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{z}}=\:\mathrm{2}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}−\mathrm{2}−\boldsymbol{\mathrm{xy}} \\ $$$$\:\:\:\frac{\mathrm{1}−\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{y}}−\mathrm{2}}\:=\:\frac{\mathrm{2}−\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{x}}−\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\:\:−\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)^{\mathrm{2}} =−\left(\mathrm{2}−\boldsymbol{\mathrm{y}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\mathrm{1}−\boldsymbol{\mathrm{x}}\:=\mathrm{2}−\boldsymbol{\mathrm{y}}\:\:\:\:\:\:\:\:\:\:\mathrm{1}−\boldsymbol{\mathrm{x}}=\:\boldsymbol{\mathrm{y}}−\mathrm{2} \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{y}}=\:\mathrm{1}−\boldsymbol{\mathrm{x}}\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{3}−\boldsymbol{\mathrm{x}} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{z}}=\:\frac{\mathrm{1}−\boldsymbol{\mathrm{x}}}{\mathrm{1}−\boldsymbol{\mathrm{x}}−\mathrm{2}}=\frac{\mathrm{1}−\boldsymbol{\mathrm{x}}}{−\mathrm{1}−\boldsymbol{\mathrm{x}}}=\frac{\boldsymbol{\mathrm{x}}−\mathrm{1}}{\boldsymbol{\mathrm{x}}+\mathrm{1}} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{z}}=\:\frac{\mathrm{2}−\mathrm{1}+\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}−\mathrm{1}}=\:\frac{\mathrm{1}+\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\frac{\boldsymbol{\mathrm{x}}−\mathrm{1}}{\boldsymbol{\mathrm{x}}+\mathrm{1}}=\frac{\boldsymbol{\mathrm{x}}+\mathrm{1}}{\boldsymbol{\mathrm{x}}−\mathrm{1}}\:\:\:\:\:\:\:\:\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)^{\mathrm{2}} =\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}−\mathrm{1}=\:−\boldsymbol{\mathrm{x}}\:−\mathrm{1}\:\:\:\mathrm{2}\boldsymbol{\mathrm{x}}=\mathrm{0}\:\:\:\:\:\boldsymbol{\mathrm{x}}=\mathrm{0} \\ $$$$\:\:\boldsymbol{\mathrm{x}}=\mathrm{0}\:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{1}\:\:\:\:\:\:\boldsymbol{\mathrm{z}}=\:−\mathrm{1} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{3}−\boldsymbol{\mathrm{x}}\:\:\:\:\:\:\boldsymbol{\mathrm{z}}=\frac{\mathrm{1}−\boldsymbol{\mathrm{x}}}{\mathrm{3}−\boldsymbol{\mathrm{x}}−\mathrm{2}}=\frac{\mathrm{1}−\boldsymbol{\mathrm{x}}}{\mathrm{1}−\boldsymbol{\mathrm{x}}}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}=\mathrm{3}−\boldsymbol{\mathrm{y}}=\:\mathrm{2}\:\:\:\:\:\:\boldsymbol{\mathrm{x}}=\mathrm{2}\:\:\boldsymbol{\mathrm{y}}=\mathrm{1}\:\:\:\:\boldsymbol{\mathrm{z}}=\mathrm{1} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{z}}=\mathrm{2}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}−\mathrm{2}−\boldsymbol{\mathrm{xy}}=\mathrm{2}\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{xy}}\:+\boldsymbol{\mathrm{y}}−\mathrm{2} \\ $$$$\:\:\boldsymbol{\mathrm{z}}=\:\boldsymbol{\mathrm{x}}\centerdot\left(\mathrm{2}−\boldsymbol{\mathrm{y}}\right)\:−\mathrm{1}\left(\mathrm{2}−\boldsymbol{\mathrm{y}}\right)\:=\:\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\left(\mathrm{2}−\boldsymbol{\mathrm{y}}\right) \\ $$$$\:\:\boldsymbol{\mathrm{z}}=\boldsymbol{\mathrm{z}}=\boldsymbol{\mathrm{z}} \\ $$$$\:\:\:\:\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\left(\mathrm{2}−\boldsymbol{\mathrm{y}}\right)=\frac{\mathrm{1}−\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{y}}−\mathrm{2}}\:\:\:\:\:\:\:\left(\mathrm{2}−\boldsymbol{\mathrm{y}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{y}}=\:\mathrm{1}\:\:\:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{3}\:\: \\ $$$$\:\:\:\:\boldsymbol{\mathrm{x}}=\mathrm{1}\:\:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{2}\:\:\:\:\:\:\:\boldsymbol{\mathrm{z}}=\mathrm{1} \\ $$$$\:\:\:\boldsymbol{\mathrm{x}}=\mathrm{0}\:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{3}\:\:\:\:\boldsymbol{\mathrm{z}}=\mathrm{1} \\ $$$$\:\:\boldsymbol{\mathrm{y}}=\mathrm{3}\:\:\:\:\boldsymbol{\mathrm{x}}=\mathrm{2}\:\:\:\:\:\boldsymbol{\mathrm{z}}=−\mathrm{1} \\ $$$$\:\:\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\left(\mathrm{2}−\boldsymbol{\mathrm{y}}\right)\:\:=\:\:\frac{\mathrm{2}−\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{x}}−\mathrm{1}} \\ $$$$\:\:\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1}\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}=\mathrm{0}\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}=\mathrm{2} \\ $$$$\:\:\boldsymbol{\mathrm{x}}=\mathrm{0}\:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{3}\:\:\:\:\:\boldsymbol{\mathrm{z}}=\mathrm{1} \\ $$$$\:\boldsymbol{\mathrm{x}}=\mathrm{2}\:\:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{1}\:\:\:\:\:\boldsymbol{\mathrm{z}}=\mathrm{1} \\ $$$$\:\:\boldsymbol{\mathrm{x}}=\mathrm{2}\:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{3}\:\:\:\:\:\:\boldsymbol{\mathrm{z}}=\:−\mathrm{1} \\ $$$$\left(\mathrm{0},\mathrm{1},−\mathrm{1}\right)\:\:\left(\mathrm{0},\mathrm{3},\mathrm{1}\right)\:\:\:\:\left(\mathrm{1},\mathrm{2},\mathrm{0}\right)\:\:\:\:\left(\mathrm{2},\mathrm{1},\mathrm{1}\right)\:\:\left(\mathrm{2},\bar {\mathrm{3}}−\mathrm{1}\right) \\ $$$$ \\ $$
Commented by universe last updated on 04/Jan/23
thanks sir
$${thanks}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *