Question Number 119821 by bemath last updated on 27/Oct/20
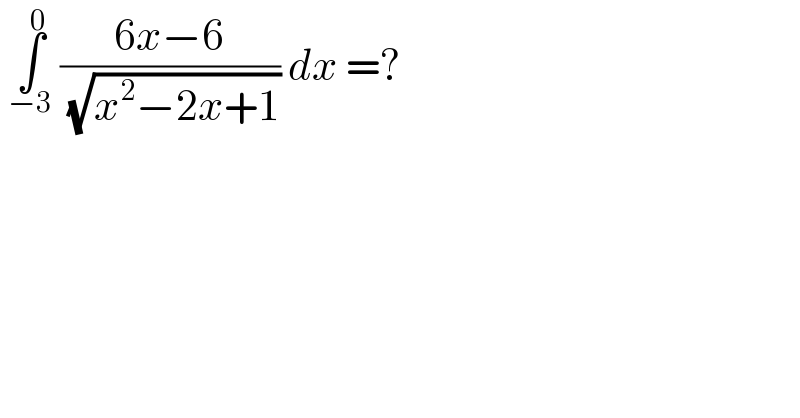
$$\:\underset{−\mathrm{3}} {\overset{\mathrm{0}} {\int}}\:\frac{\mathrm{6}{x}−\mathrm{6}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}}\:{dx}\:=? \\ $$
Answered by bobhans last updated on 27/Oct/20
![∫_(−3) ^0 ((6(x−1))/( (√((x−1)^2 )))) dx =∫_(−3) ^0 ((6(x−1))/(∣x−1∣)) dx = −6∫_(−3) ^0 dx = −6(x)] _(−3)^0 = −6(0+3)=−18](https://www.tinkutara.com/question/Q119826.png)
$$\:\underset{−\mathrm{3}} {\overset{\mathrm{0}} {\int}}\:\frac{\mathrm{6}\left({x}−\mathrm{1}\right)}{\:\sqrt{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }}\:{dx}\:=\underset{−\mathrm{3}} {\overset{\mathrm{0}} {\int}}\:\frac{\mathrm{6}\left({x}−\mathrm{1}\right)}{\mid{x}−\mathrm{1}\mid}\:{dx} \\ $$$$\left.=\:−\mathrm{6}\underset{−\mathrm{3}} {\overset{\mathrm{0}} {\int}}{dx}\:=\:−\mathrm{6}\left({x}\right)\right]\:_{−\mathrm{3}} ^{\mathrm{0}} \:=\:−\mathrm{6}\left(\mathrm{0}+\mathrm{3}\right)=−\mathrm{18} \\ $$
Answered by Olaf last updated on 27/Oct/20
![x^2 −2x+1 is defined for x∈[−3;0] I = ∫_(−3) ^0 ((6(x−1))/( (√((x^2 −1)^2 ))))dx I = ∫_(−3) ^0 ((6(x−1))/( ∣x−1∣))dx I = ∫_(−3) ^0 ((6(x−1))/( 1−x))dx = −6(0+3) = −18](https://www.tinkutara.com/question/Q119828.png)
$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:{x}\in\left[−\mathrm{3};\mathrm{0}\right] \\ $$$$\mathrm{I}\:=\:\int_{−\mathrm{3}} ^{\mathrm{0}} \frac{\mathrm{6}\left({x}−\mathrm{1}\right)}{\:\sqrt{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }}{dx} \\ $$$$\mathrm{I}\:=\:\int_{−\mathrm{3}} ^{\mathrm{0}} \frac{\mathrm{6}\left({x}−\mathrm{1}\right)}{\:\mid{x}−\mathrm{1}\mid}{dx} \\ $$$$\mathrm{I}\:=\:\int_{−\mathrm{3}} ^{\mathrm{0}} \frac{\mathrm{6}\left({x}−\mathrm{1}\right)}{\:\mathrm{1}−{x}}{dx}\:=\:−\mathrm{6}\left(\mathrm{0}+\mathrm{3}\right)\:=\:−\mathrm{18} \\ $$
Answered by 1549442205PVT last updated on 27/Oct/20
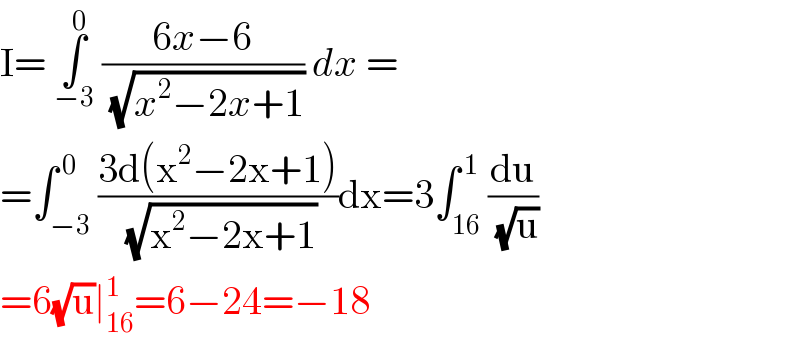
$$\mathrm{I}=\:\underset{−\mathrm{3}} {\overset{\mathrm{0}} {\int}}\:\frac{\mathrm{6}{x}−\mathrm{6}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}}\:{dx}\:= \\ $$$$=\int_{−\mathrm{3}} ^{\:\mathrm{0}} \frac{\mathrm{3d}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}\right)}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}}\mathrm{dx}=\mathrm{3}\int_{\mathrm{16}} ^{\:\mathrm{1}} \frac{\mathrm{du}}{\:\sqrt{\mathrm{u}}} \\ $$$$=\mathrm{6}\sqrt{\mathrm{u}}\mid_{\mathrm{16}} ^{\mathrm{1}} =\mathrm{6}−\mathrm{24}=−\mathrm{18} \\ $$
