Question Number 120275 by bramlexs22 last updated on 30/Oct/20
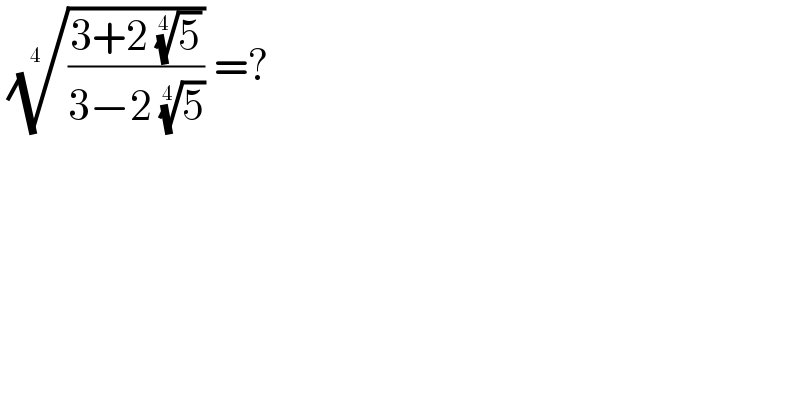
$$\:\sqrt[{\mathrm{4}\:}]{\frac{\mathrm{3}+\mathrm{2}\:\sqrt[{\mathrm{4}}]{\mathrm{5}}}{\mathrm{3}−\mathrm{2}\:\sqrt[{\mathrm{4}}]{\mathrm{5}}}}\:=?\: \\ $$
Answered by TANMAY PANACEA last updated on 30/Oct/20
![3−2(5)^(1/4) =3−(2^4 ×5)^(1/4) =3−(80)^(1/4) =(81)^(1/4) −(80)^(1/4) =a−b 3+2(5)^(1/4) =(81)^(1/4) +(80)^(1/4) =a+b [a=(81)^(1/4) b=(80)^(1/4) ] (((a+b)/(a−b)))^(1/4) ={(((a+b)^2 )/(a^2 −b^2 ))}^(1/4) ={(((81)^(1/2) +2(81)^(1/4) (80)^(1/4) +(80)^(1/2) )/((81)^(1/2) −(80)^(1/2) ))}^(1/4) ={(((81)^(1/2) +(80)^(1/2) )/(81−80))×(((81)^(1/2) +2(81)^(1/4) (80)^(1/4) +(80)^(1/2) )/1)}^(1/4) ={((a^2 +b^2 )/1)×((a^2 +2ab+b^2 )/1)}^(1/4) =(a^2 +b^2 )^(1/4) ×(a+b)^(1/2) ={(81)^(1/2) +(80)^(1/2) }^(1/4) ×{(81)^(1/4) +(80)^(1/4) }^(1/2) =(9+4(√5) )^(1/4) ×{3+2×(5)^(1/4) }^(1/2) =(2^2 +5+2×2×(√5) }^(1/4) ×(3+2×5^(1/4) )^(1/2) =(2+(√5) )^(1/2) ×(3+2×5^(1/4) )^(1/2) =(6+4×5^(1/4) +3×5^(1/2) +2×5^(3/4) )^(1/2) wait...](https://www.tinkutara.com/question/Q120343.png)
$$\mathrm{3}−\mathrm{2}\left(\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\mathrm{3}−\left(\mathrm{2}^{\mathrm{4}} ×\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\mathrm{3}−\left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} −\left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} ={a}−{b} \\ $$$$\mathrm{3}+\mathrm{2}\left(\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} =\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} +\left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} ={a}+{b}\:\:\left[{a}=\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:\:{b}=\left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \right] \\ $$$$\left(\frac{{a}+{b}}{{a}−{b}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\left\{\frac{\left({a}+{b}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right\}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\left\{\frac{\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{2}\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} +\left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} −\left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\right\}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\left\{\frac{\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +\left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{81}−\mathrm{80}}×\frac{\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{2}\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} +\left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}}\right\}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\left\{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{1}}×\frac{{a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} }{\mathrm{1}}\right\}^{\frac{\mathrm{1}}{\mathrm{4}}} =\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} ×\left({a}+{b}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left\{\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +\left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right\}^{\frac{\mathrm{1}}{\mathrm{4}}} ×\left\{\left(\mathrm{81}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} +\left(\mathrm{80}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \right\}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left(\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}\:\right)^{\frac{\mathrm{1}}{\mathrm{4}}} ×\left\{\mathrm{3}+\mathrm{2}×\left(\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \right\}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left(\mathrm{2}^{\mathrm{2}} +\mathrm{5}+\mathrm{2}×\mathrm{2}×\sqrt{\mathrm{5}}\:\right\}^{\frac{\mathrm{1}}{\mathrm{4}}} ×\left(\mathrm{3}+\mathrm{2}×\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left(\mathrm{2}+\sqrt{\mathrm{5}}\:\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ×\left(\mathrm{3}+\mathrm{2}×\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left(\mathrm{6}+\mathrm{4}×\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{3}×\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{2}×\mathrm{5}^{\frac{\mathrm{3}}{\mathrm{4}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${wait}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
