Question Number 124672 by sdfg last updated on 05/Dec/20
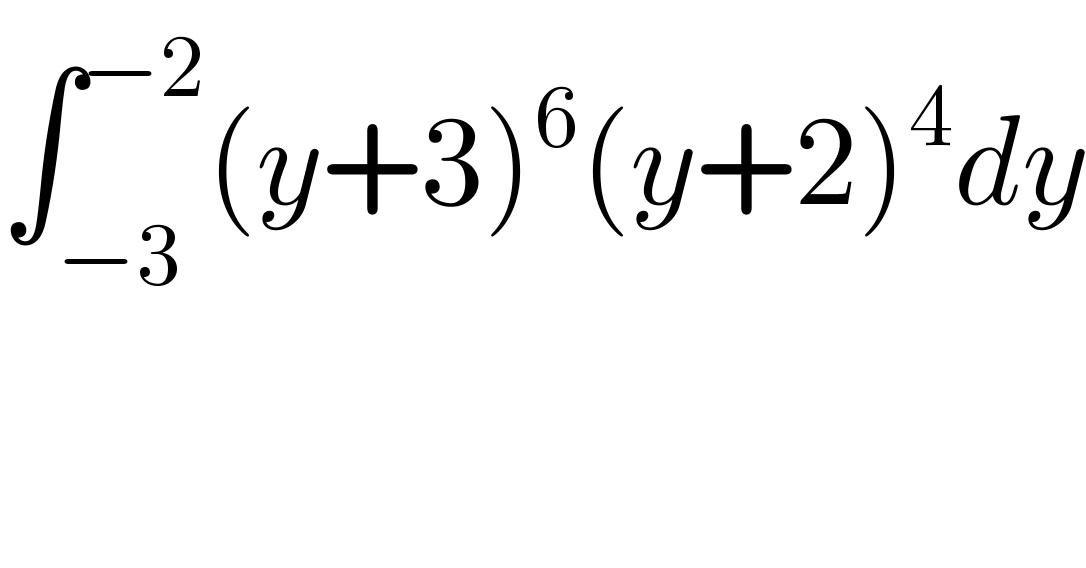
$$\int_{−\mathrm{3}} ^{−\mathrm{2}} \left({y}+\mathrm{3}\right)^{\mathrm{6}} \left({y}+\mathrm{2}\right)^{\mathrm{4}} {dy} \\ $$
Commented by mohammad17 last updated on 05/Dec/20

$${put}:{n}={y}+\mathrm{3}\Rightarrow{y}={n}−\mathrm{3}\Rightarrow{dy}={dn} \\ $$$$ \\ $$$${y}=−\mathrm{2}\Rightarrow{n}=\mathrm{1}\:\:,\:\:\:{y}=−\mathrm{3}\Rightarrow{n}=\mathrm{0} \\ $$$$ \\ $$$$\therefore\int_{−\mathrm{3}} ^{\:−\mathrm{2}} \left({y}+\mathrm{3}\right)^{\mathrm{6}} \left({y}+\mathrm{2}\right)^{\mathrm{4}} {dy}= \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} {n}^{\mathrm{6}} \left({n}−\mathrm{1}\right)^{\mathrm{4}} {dn}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left({n}^{\mathrm{10}} −\mathrm{4}{n}^{\mathrm{9}} +\mathrm{6}{n}^{\mathrm{8}} −\mathrm{4}{n}^{\mathrm{7}} +{n}^{\mathrm{6}} \right){dn} \\ $$$$ \\ $$$$=\left(\frac{{n}^{\mathrm{11}} }{\mathrm{11}}−\frac{\mathrm{2}{n}^{\mathrm{10}} }{\mathrm{5}}+\frac{\mathrm{2}{n}^{\mathrm{9}} }{\mathrm{3}}−\frac{{n}^{\mathrm{8}} }{\mathrm{2}}+\frac{{n}^{\mathrm{7}} }{\mathrm{7}}\right)_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{11}}−\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{7}}=\frac{\mathrm{1}}{\mathrm{2310}} \\ $$$$ \\ $$$$\left({mohammad}\:{Aldolaimy}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 05/Dec/20
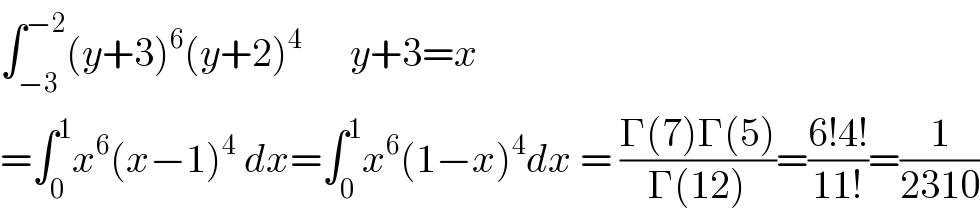
$$\int_{−\mathrm{3}} ^{−\mathrm{2}} \left({y}+\mathrm{3}\right)^{\mathrm{6}} \left({y}+\mathrm{2}\right)^{\mathrm{4}} \:\:\:\:\:\:{y}+\mathrm{3}={x} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{6}} \left({x}−\mathrm{1}\right)^{\mathrm{4}} \:{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{6}} \left(\mathrm{1}−{x}\right)^{\mathrm{4}} {dx}\:=\:\frac{\Gamma\left(\mathrm{7}\right)\Gamma\left(\mathrm{5}\right)}{\Gamma\left(\mathrm{12}\right)}=\frac{\mathrm{6}!\mathrm{4}!}{\mathrm{11}!}=\frac{\mathrm{1}}{\mathrm{2310}} \\ $$
