Question Number 89702 by 974342176 last updated on 18/Apr/20
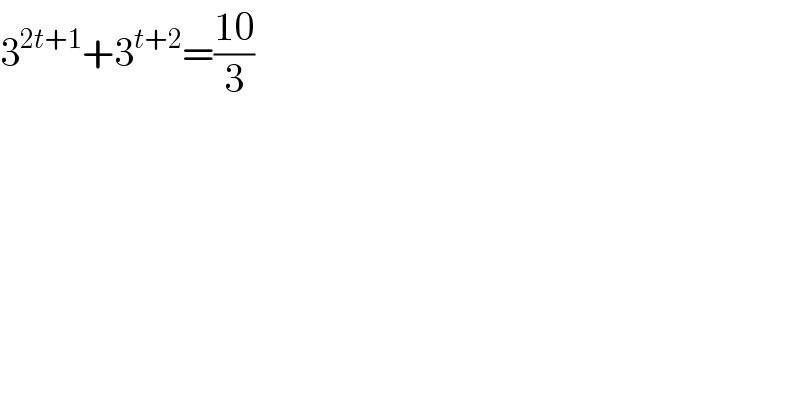
$$\mathrm{3}^{\mathrm{2}{t}+\mathrm{1}} +\mathrm{3}^{{t}+\mathrm{2}} =\frac{\mathrm{10}}{\mathrm{3}} \\ $$
Answered by Kunal12588 last updated on 18/Apr/20
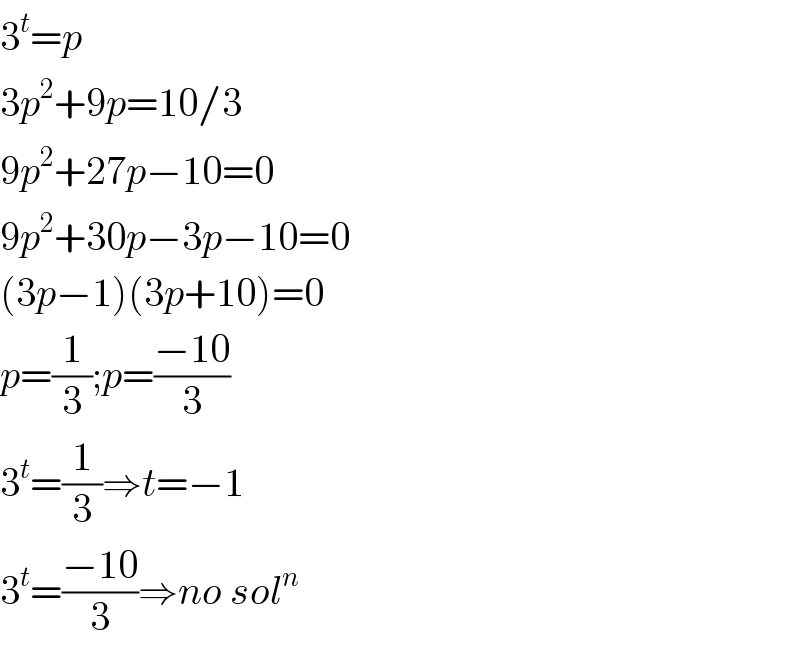
$$\mathrm{3}^{{t}} ={p} \\ $$$$\mathrm{3}{p}^{\mathrm{2}} +\mathrm{9}{p}=\mathrm{10}/\mathrm{3} \\ $$$$\mathrm{9}{p}^{\mathrm{2}} +\mathrm{27}{p}−\mathrm{10}=\mathrm{0} \\ $$$$\mathrm{9}{p}^{\mathrm{2}} +\mathrm{30}{p}−\mathrm{3}{p}−\mathrm{10}=\mathrm{0} \\ $$$$\left(\mathrm{3}{p}−\mathrm{1}\right)\left(\mathrm{3}{p}+\mathrm{10}\right)=\mathrm{0} \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{3}};{p}=\frac{−\mathrm{10}}{\mathrm{3}} \\ $$$$\mathrm{3}^{{t}} =\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{t}=−\mathrm{1} \\ $$$$\mathrm{3}^{{t}} =\frac{−\mathrm{10}}{\mathrm{3}}\Rightarrow{no}\:{sol}^{{n}} \\ $$
Commented by MJS last updated on 18/Apr/20

$$\mathrm{right}\:\mathrm{path}\:\mathrm{wrong}\:\mathrm{conclusion} \\ $$$$\mathrm{3}^{{t}} ={p}\:\Leftrightarrow\:{t}=\frac{\mathrm{ln}\:{p}}{\mathrm{ln}\:\mathrm{3}} \\ $$$${p}=−\frac{\mathrm{10}}{\mathrm{3}}\vee{p}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow \\ $$$${t}=\frac{\mathrm{ln}\:−\frac{\mathrm{10}}{\mathrm{3}}}{\mathrm{ln}\:\mathrm{3}}\:\notin\mathbb{R}\vee\:{t}=\frac{\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{ln}\:\mathrm{3}}=−\mathrm{1} \\ $$$$\bullet\:\mathrm{solution}:\:{t}=−\mathrm{1}\:\bullet \\ $$$$\left({t}=\frac{\mathrm{ln}\:\frac{\mathrm{10}}{\mathrm{3}}}{\mathrm{ln}\:\mathrm{3}}+\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{ln}\:\mathrm{3}}\pi\mathrm{i}\:\in\mathbb{C}\right) \\ $$
