Question Number 89271 by jagoll last updated on 16/Apr/20
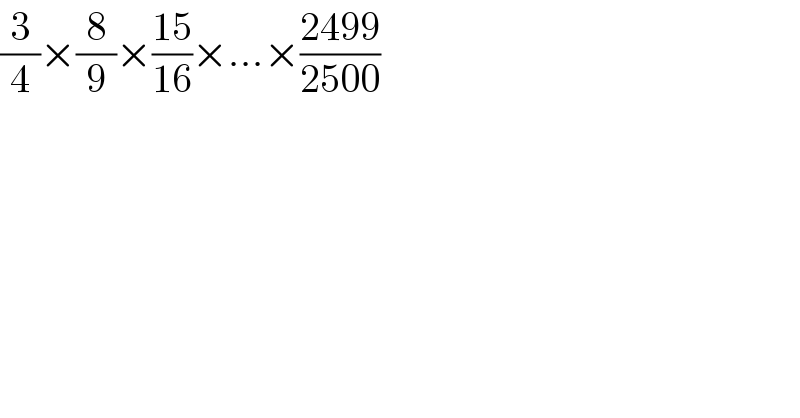
$$\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{8}}{\mathrm{9}}×\frac{\mathrm{15}}{\mathrm{16}}×…×\frac{\mathrm{2499}}{\mathrm{2500}} \\ $$
Commented by john santu last updated on 16/Apr/20
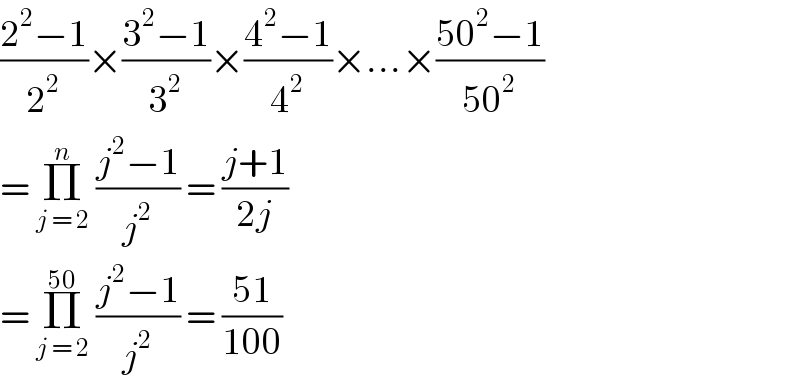
$$\frac{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }×\frac{\mathrm{3}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }×\frac{\mathrm{4}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }×…×\frac{\mathrm{50}^{\mathrm{2}} −\mathrm{1}}{\mathrm{50}^{\mathrm{2}} } \\ $$$$=\:\underset{{j}\:=\:\mathrm{2}} {\overset{{n}} {\prod}}\:\frac{{j}^{\mathrm{2}} −\mathrm{1}}{{j}^{\mathrm{2}} }\:=\:\frac{{j}+\mathrm{1}}{\mathrm{2}{j}} \\ $$$$=\:\underset{{j}\:=\:\mathrm{2}} {\overset{\mathrm{50}} {\prod}}\:\frac{{j}^{\mathrm{2}} −\mathrm{1}}{{j}^{\mathrm{2}} }\:=\:\frac{\mathrm{51}}{\mathrm{100}} \\ $$
