Question Number 39029 by MJS last updated on 01/Jul/18
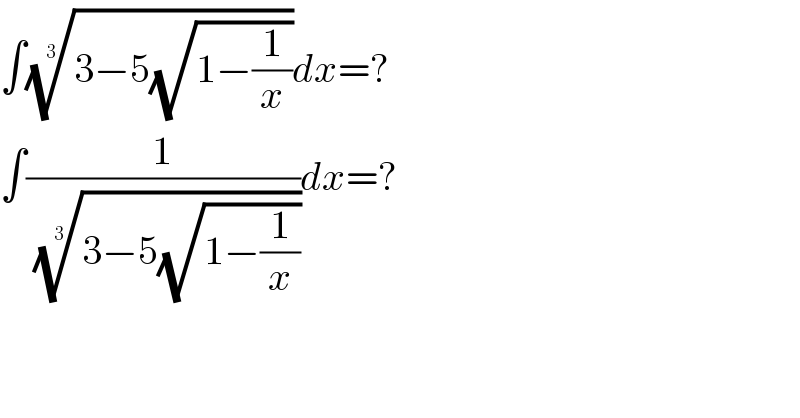
$$\int\sqrt[{\mathrm{3}}]{\mathrm{3}−\mathrm{5}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}}{dx}=? \\ $$$$\int\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}−\mathrm{5}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}}}{dx}=? \\ $$
Answered by MJS last updated on 02/Jul/18
![∫((3−5(√(1−(1/x)))))^(1/3) dx= [t=−3+5(√(1−(1/x))) → dx=(2/5)x^2 (√(1−(1/x)))dt] =−50∫(((t+3)(t)^(1/3) )/((t−2)^2 (t+8)^2 ))dt= [u=(t)^(1/3) → dt=3(u^2 )^(1/3) du] =−150∫((u^3 (u^3 +3))/((u^3 −2)^2 (u^3 +8)^2 ))du= [((Ostrogradski′s Method)),((∫(p/q)=(p_1 /q_1 )+∫(p_2 /q_2 ))),((q_1 =gcd(q, q′); q_2 =(q/q_1 ))),((we get p_1 , p_2 by matching constants of)),(((p/q)=(d/du)((p_1 /q_1 ))+(p_2 /q_2 ))),((p=u^3 (u^3 +3); q=(u^3 −2)^2 (u^3 +8)^2 )),((q′=6u^2 (u^3 −2)(u^3 +8)(2u^3 +6))),((q_1 =q_2 =(u^3 −2)(u^3 +8))),((p_1 =−(u/6); p_2 =(1/6))) ] =25(u/((u^3 −2)(u^3 +8)))−25∫(du/((u^3 −2)(u^3 +8))) ∫(du/((u^3 −2)(u^3 +8)))=∫(du/((u^3 −2)(u^2 −2u+4)(u+2)))= =(1/(10))∫(du/(u^3 −2))+(1/(120))∫((u−4)/(u^2 −2u+4))du−(1/(120))∫(du/(u+2)) ∫(du/(u+2))=ln∣u+2∣ ∫((u−4)/(u^2 −2u+4))du=(1/2)∫((2u−2)/(u^2 −2u+4))du−3∫(du/(u^2 −2u+4))= [∫((ax+b)/(ax^2 +bx+c))dx=ln∣ax^2 +bx+c∣] [∫(dx/(ax^2 +bx+c))=(2/( (√(4ac−b^2 ))))arctan ((2ax+b)/( (√(4ac−b^2 ))))] (1/2)ln∣u^2 −2u+4∣−(√3)arctan ((√3)/3)(u−1) ∫(du/(u^3 −2))=∫(du/((u−(2)^(1/3) )(u^2 +(2)^(1/3) u+(4)^(1/3) )))= =((2)^(1/3) /6)(∫(du/(u−(2)^(1/3) ))−∫((u+(4)^(1/3) )/(u^2 +(2)^(1/3) u+(4)^(1/3) ))du)= =((2)^(1/3) /6)(∫(du/(u−(2)^(1/3) ))−(1/2)∫((2u+(2)^(1/3) )/(u^2 +(2)^(1/3) u+(4)^(1/3) ))−((3(2)^(1/3) )/2)∫(du/(u^2 +(2)^(1/3) u+(4)^(1/3) )))= =((2)^(1/3) /6)(ln∣u−(2)^(1/3) ∣−(1/2)ln∣u^2 +(2)^(1/3) u+(4)^(1/3) ∣−(√3)arctan ((√3)/3)((4)^(1/3) u+1)) =−((5(2)^(1/3) )/(12))(ln∣u−(2)^(1/3) ∣−(1/2)ln∣u^2 +(2)^(1/3) u+(4)^(1/3) ∣−(√3)arctan ((√3)/3)((4)^(1/3) u+1))− −(5/(48))ln∣u^2 −2u+4∣−((5(√3))/(24))arctan ((√3)/3)(u−1)+ +(5/(24))ln∣u+2∣+25(u/((u^3 −2)(u^3 +8)))+C u=(t)^(1/3) t=−3+5(√(1−(1/x))) too lazy to insert these... but it′s solved](https://www.tinkutara.com/question/Q39068.png)
$$\int\sqrt[{\mathrm{3}}]{\mathrm{3}−\mathrm{5}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=−\mathrm{3}+\mathrm{5}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}\:\rightarrow\:{dx}=\frac{\mathrm{2}}{\mathrm{5}}{x}^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}{dt}\right] \\ $$$$=−\mathrm{50}\int\frac{\left({t}+\mathrm{3}\right)\sqrt[{\mathrm{3}}]{{t}}}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} \left({t}+\mathrm{8}\right)^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\sqrt[{\mathrm{3}}]{{t}}\:\rightarrow\:{dt}=\mathrm{3}\sqrt[{\mathrm{3}}]{{u}^{\mathrm{2}} }{du}\right] \\ $$$$=−\mathrm{150}\int\frac{{u}^{\mathrm{3}} \left({u}^{\mathrm{3}} +\mathrm{3}\right)}{\left({u}^{\mathrm{3}} −\mathrm{2}\right)^{\mathrm{2}} \left({u}^{\mathrm{3}} +\mathrm{8}\right)^{\mathrm{2}} }{du}= \\ $$$$\:\:\:\:\:\begin{bmatrix}{\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}}\\{\int\frac{{p}}{{q}}=\frac{{p}_{\mathrm{1}} }{{q}_{\mathrm{1}} }+\int\frac{{p}_{\mathrm{2}} }{{q}_{\mathrm{2}} }}\\{{q}_{\mathrm{1}} =\mathrm{gcd}\left({q},\:{q}'\right);\:{q}_{\mathrm{2}} =\frac{{q}}{{q}_{\mathrm{1}} }}\\{\mathrm{we}\:\mathrm{get}\:{p}_{\mathrm{1}} ,\:{p}_{\mathrm{2}} \:\mathrm{by}\:\mathrm{matching}\:\mathrm{constants}\:\mathrm{of}}\\{\frac{{p}}{{q}}=\frac{{d}}{{du}}\left(\frac{{p}_{\mathrm{1}} }{{q}_{\mathrm{1}} }\right)+\frac{{p}_{\mathrm{2}} }{{q}_{\mathrm{2}} }}\\{{p}={u}^{\mathrm{3}} \left({u}^{\mathrm{3}} +\mathrm{3}\right);\:{q}=\left({u}^{\mathrm{3}} −\mathrm{2}\right)^{\mathrm{2}} \left({u}^{\mathrm{3}} +\mathrm{8}\right)^{\mathrm{2}} }\\{{q}'=\mathrm{6}{u}^{\mathrm{2}} \left({u}^{\mathrm{3}} −\mathrm{2}\right)\left({u}^{\mathrm{3}} +\mathrm{8}\right)\left(\mathrm{2}{u}^{\mathrm{3}} +\mathrm{6}\right)}\\{{q}_{\mathrm{1}} ={q}_{\mathrm{2}} =\left({u}^{\mathrm{3}} −\mathrm{2}\right)\left({u}^{\mathrm{3}} +\mathrm{8}\right)}\\{{p}_{\mathrm{1}} =−\frac{{u}}{\mathrm{6}};\:{p}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}}}\end{bmatrix} \\ $$$$=\mathrm{25}\frac{{u}}{\left({u}^{\mathrm{3}} −\mathrm{2}\right)\left({u}^{\mathrm{3}} +\mathrm{8}\right)}−\mathrm{25}\int\frac{{du}}{\left({u}^{\mathrm{3}} −\mathrm{2}\right)\left({u}^{\mathrm{3}} +\mathrm{8}\right)} \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{{du}}{\left({u}^{\mathrm{3}} −\mathrm{2}\right)\left({u}^{\mathrm{3}} +\mathrm{8}\right)}=\int\frac{{du}}{\left({u}^{\mathrm{3}} −\mathrm{2}\right)\left({u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{4}\right)\left({u}+\mathrm{2}\right)}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{10}}\int\frac{{du}}{{u}^{\mathrm{3}} −\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{120}}\int\frac{{u}−\mathrm{4}}{{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{4}}{du}−\frac{\mathrm{1}}{\mathrm{120}}\int\frac{{du}}{{u}+\mathrm{2}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\int\frac{{du}}{{u}+\mathrm{2}}=\mathrm{ln}\mid{u}+\mathrm{2}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\int\frac{{u}−\mathrm{4}}{{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{4}}{du}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{u}−\mathrm{2}}{{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{4}}{du}−\mathrm{3}\int\frac{{du}}{{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{4}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\int\frac{{ax}+{b}}{{ax}^{\mathrm{2}} +{bx}+{c}}{dx}=\mathrm{ln}\mid{ax}^{\mathrm{2}} +{bx}+{c}\mid\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\int\frac{{dx}}{{ax}^{\mathrm{2}} +{bx}+{c}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}\mathrm{arctan}\:\frac{\mathrm{2}{ax}+{b}}{\:\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{4}\mid−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left({u}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\int\frac{{du}}{{u}^{\mathrm{3}} −\mathrm{2}}=\int\frac{{du}}{\left({u}−\sqrt[{\mathrm{3}}]{\mathrm{2}}\right)\left({u}^{\mathrm{2}} +\sqrt[{\mathrm{3}}]{\mathrm{2}}{u}+\sqrt[{\mathrm{3}}]{\mathrm{4}}\right)}= \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{6}}\left(\int\frac{{du}}{{u}−\sqrt[{\mathrm{3}}]{\mathrm{2}}}−\int\frac{{u}+\sqrt[{\mathrm{3}}]{\mathrm{4}}}{{u}^{\mathrm{2}} +\sqrt[{\mathrm{3}}]{\mathrm{2}}{u}+\sqrt[{\mathrm{3}}]{\mathrm{4}}}{du}\right)= \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{6}}\left(\int\frac{{du}}{{u}−\sqrt[{\mathrm{3}}]{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{u}+\sqrt[{\mathrm{3}}]{\mathrm{2}}}{{u}^{\mathrm{2}} +\sqrt[{\mathrm{3}}]{\mathrm{2}}{u}+\sqrt[{\mathrm{3}}]{\mathrm{4}}}−\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}}\int\frac{{du}}{{u}^{\mathrm{2}} +\sqrt[{\mathrm{3}}]{\mathrm{2}}{u}+\sqrt[{\mathrm{3}}]{\mathrm{4}}}\right)= \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{6}}\left(\mathrm{ln}\mid{u}−\sqrt[{\mathrm{3}}]{\mathrm{2}}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid{u}^{\mathrm{2}} +\sqrt[{\mathrm{3}}]{\mathrm{2}}{u}+\sqrt[{\mathrm{3}}]{\mathrm{4}}\mid−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\sqrt[{\mathrm{3}}]{\mathrm{4}}{u}+\mathrm{1}\right)\right) \\ $$$$ \\ $$$$\:\:\:\:\:=−\frac{\mathrm{5}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{12}}\left(\mathrm{ln}\mid{u}−\sqrt[{\mathrm{3}}]{\mathrm{2}}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid{u}^{\mathrm{2}} +\sqrt[{\mathrm{3}}]{\mathrm{2}}{u}+\sqrt[{\mathrm{3}}]{\mathrm{4}}\mid−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\sqrt[{\mathrm{3}}]{\mathrm{4}}{u}+\mathrm{1}\right)\right)− \\ $$$$\:\:\:\:\:−\frac{\mathrm{5}}{\mathrm{48}}\mathrm{ln}\mid{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{4}\mid−\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{24}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left({u}−\mathrm{1}\right)+ \\ $$$$\:\:\:\:\:+\frac{\mathrm{5}}{\mathrm{24}}\mathrm{ln}\mid{u}+\mathrm{2}\mid+\mathrm{25}\frac{{u}}{\left({u}^{\mathrm{3}} −\mathrm{2}\right)\left({u}^{\mathrm{3}} +\mathrm{8}\right)}+{C} \\ $$$${u}=\sqrt[{\mathrm{3}}]{{t}} \\ $$$${t}=−\mathrm{3}+\mathrm{5}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}} \\ $$$$\mathrm{too}\:\mathrm{lazy}\:\mathrm{to}\:\mathrm{insert}\:\mathrm{these}…\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{solved} \\ $$
Commented by maxmathsup by imad last updated on 02/Jul/18
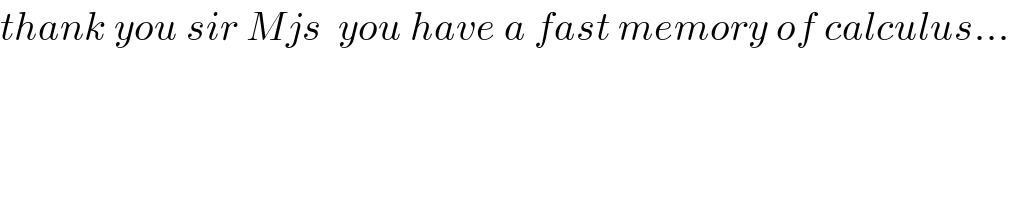
$${thank}\:{you}\:{sir}\:{Mjs}\:\:{you}\:{have}\:{a}\:{fast}\:{memory}\:{of}\:{calculus}… \\ $$
Answered by MJS last updated on 02/Jul/18
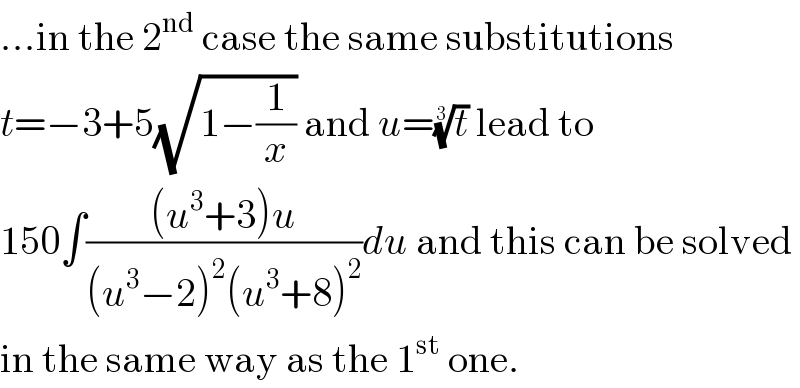
$$…\mathrm{in}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{case}\:\mathrm{the}\:\mathrm{same}\:\mathrm{substitutions} \\ $$$${t}=−\mathrm{3}+\mathrm{5}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}\:\mathrm{and}\:{u}=\sqrt[{\mathrm{3}}]{{t}}\:\mathrm{lead}\:\mathrm{to} \\ $$$$\mathrm{150}\int\frac{\left({u}^{\mathrm{3}} +\mathrm{3}\right){u}}{\left({u}^{\mathrm{3}} −\mathrm{2}\right)^{\mathrm{2}} \left({u}^{\mathrm{3}} +\mathrm{8}\right)^{\mathrm{2}} }{du}\:\mathrm{and}\:\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{same}\:\mathrm{way}\:\mathrm{as}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{one}. \\ $$
