Question Number 181466 by SEKRET last updated on 25/Nov/22
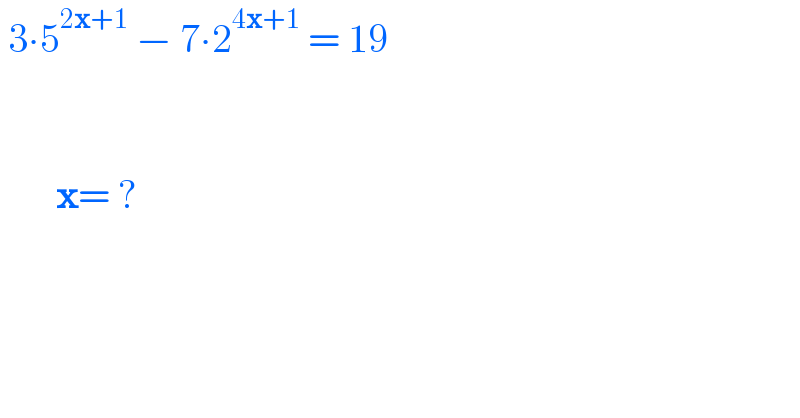
$$\:\mathrm{3}\centerdot\mathrm{5}^{\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{1}} \:−\:\mathrm{7}\centerdot\mathrm{2}^{\mathrm{4}\boldsymbol{\mathrm{x}}+\mathrm{1}} \:=\:\mathrm{19} \\ $$$$ \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}=\:? \\ $$$$ \\ $$$$ \\ $$
Answered by MJS_new last updated on 25/Nov/22
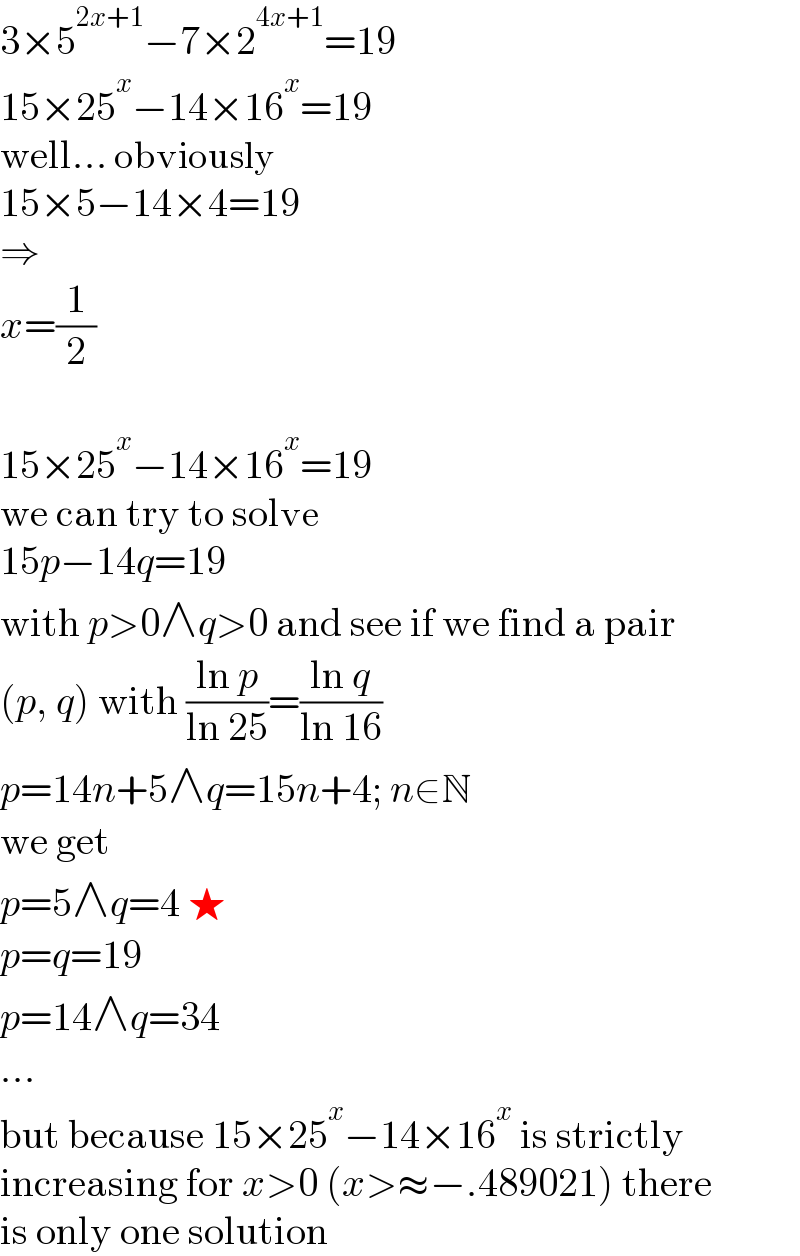
$$\mathrm{3}×\mathrm{5}^{\mathrm{2}{x}+\mathrm{1}} −\mathrm{7}×\mathrm{2}^{\mathrm{4}{x}+\mathrm{1}} =\mathrm{19} \\ $$$$\mathrm{15}×\mathrm{25}^{{x}} −\mathrm{14}×\mathrm{16}^{{x}} =\mathrm{19} \\ $$$$\mathrm{well}…\:\mathrm{obviously} \\ $$$$\mathrm{15}×\mathrm{5}−\mathrm{14}×\mathrm{4}=\mathrm{19} \\ $$$$\Rightarrow \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{15}×\mathrm{25}^{{x}} −\mathrm{14}×\mathrm{16}^{{x}} =\mathrm{19} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{try}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{15}{p}−\mathrm{14}{q}=\mathrm{19} \\ $$$$\mathrm{with}\:{p}>\mathrm{0}\wedge{q}>\mathrm{0}\:\mathrm{and}\:\mathrm{see}\:\mathrm{if}\:\mathrm{we}\:\mathrm{find}\:\mathrm{a}\:\mathrm{pair} \\ $$$$\left({p},\:{q}\right)\:\mathrm{with}\:\frac{\mathrm{ln}\:{p}}{\mathrm{ln}\:\mathrm{25}}=\frac{\mathrm{ln}\:{q}}{\mathrm{ln}\:\mathrm{16}} \\ $$$${p}=\mathrm{14}{n}+\mathrm{5}\wedge{q}=\mathrm{15}{n}+\mathrm{4};\:{n}\in\mathbb{N} \\ $$$$\mathrm{we}\:\mathrm{get} \\ $$$${p}=\mathrm{5}\wedge{q}=\mathrm{4}\:\bigstar \\ $$$${p}={q}=\mathrm{19} \\ $$$${p}=\mathrm{14}\wedge{q}=\mathrm{34} \\ $$$$… \\ $$$$\mathrm{but}\:\mathrm{because}\:\mathrm{15}×\mathrm{25}^{{x}} −\mathrm{14}×\mathrm{16}^{{x}} \:\mathrm{is}\:\mathrm{strictly} \\ $$$$\mathrm{increasing}\:\mathrm{for}\:{x}>\mathrm{0}\:\left({x}>\approx−.\mathrm{489021}\right)\:\mathrm{there} \\ $$$$\mathrm{is}\:\mathrm{only}\:\mathrm{one}\:\mathrm{solution} \\ $$
Commented by SEKRET last updated on 25/Nov/22

$$\:\:\boldsymbol{\mathrm{thanks}}\:\boldsymbol{\mathrm{sir}}! \\ $$
