Menu Close

3-8-15-24-35-find-sum-of-50-th-term-

Tinku Tara 0 Comments
Pin




Question Number 104821 by bobhans last updated on 24/Jul/20
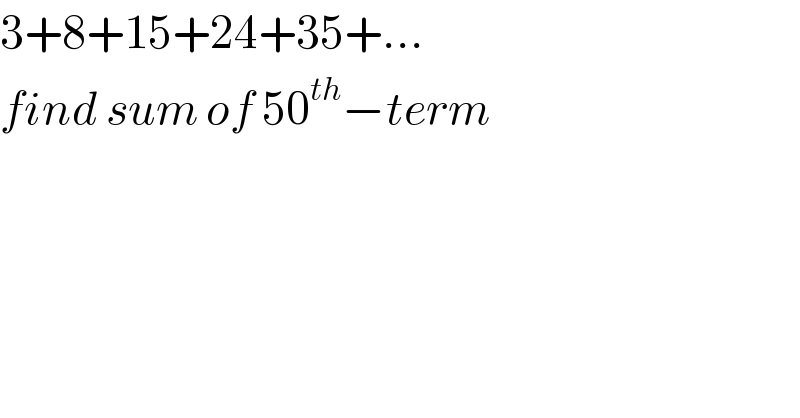
3+8+15+24+35+... find sum of 50^(th) −term
$$\mathrm{3}+\mathrm{8}+\mathrm{15}+\mathrm{24}+\mathrm{35}+…\: \\ $$$${find}\:{sum}\:{of}\:\mathrm{50}^{{th}} −{term}\: \\ $$
Answered by bemath last updated on 24/Jul/20
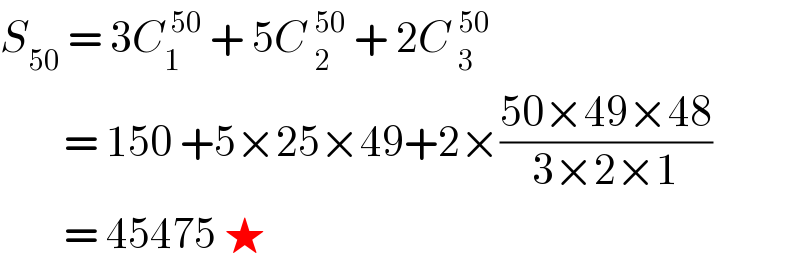
S_(50) = 3C_1 ^( 50) + 5C _2^(50) + 2C _3^(50) = 150 +5×25×49+2×((50×49×48)/(3×2×1)) = 45475 ★
$${S}_{\mathrm{50}} \:=\:\mathrm{3}{C}_{\mathrm{1}} ^{\:\mathrm{50}} \:+\:\mathrm{5}{C}\:_{\mathrm{2}} ^{\mathrm{50}} \:+\:\mathrm{2}{C}\:_{\mathrm{3}} ^{\mathrm{50}} \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{150}\:+\mathrm{5}×\mathrm{25}×\mathrm{49}+\mathrm{2}×\frac{\mathrm{50}×\mathrm{49}×\mathrm{48}}{\mathrm{3}×\mathrm{2}×\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{45475}\:\bigstar\: \\ $$
Commented by bobhans last updated on 24/Jul/20
thank you
$${thank}\:{you} \\ $$
Answered by 1549442205PVT last updated on 24/Jul/20
Since 8−3=5,15−8=7,24−15=9,35−24=11 and 5,7,9,11...form an arithmetic progress, u_n =an^2 +bn+c,so { ((u_1 =3=a+b+c(1))),((u_2 =8=4a+2b+c(2)⇒ { ((3a+b=5(4))),((5a+b=7(5))) :})),((u_3 =15=9a+3b+c(3))) :} ⇒2a=2⇒a=1⇒b=2,c=0 u_n =n^2 +2n⇒u_(50) =50^2 +2×50=2600 S_n =Σ_(k=1) ^(n) (k^2 +2k)=Σ_(k=1) ^(n) k^2 +2Σ_(l=1) ^(n) k=((n(n+1)(2n+1))/6)+n(n+1) =((n(n+1)(2n+7))/6).Therefore, S_(50) =((50×51×107)/6)=25×17×107=45475
$$\mathrm{Since}\:\mathrm{8}−\mathrm{3}=\mathrm{5},\mathrm{15}−\mathrm{8}=\mathrm{7},\mathrm{24}−\mathrm{15}=\mathrm{9},\mathrm{35}−\mathrm{24}=\mathrm{11} \\ $$$$\mathrm{and}\:\mathrm{5},\mathrm{7},\mathrm{9},\mathrm{11}…\mathrm{form}\:\mathrm{an}\:\mathrm{arithmetic}\:\mathrm{progress}, \\ $$$$\mathrm{u}_{\mathrm{n}} =\mathrm{an}^{\mathrm{2}} +\mathrm{bn}+\mathrm{c},\mathrm{so} \\ $$$$\begin{cases}{\mathrm{u}_{\mathrm{1}} =\mathrm{3}=\mathrm{a}+\mathrm{b}+\mathrm{c}\left(\mathrm{1}\right)}\\{\mathrm{u}_{\mathrm{2}} =\mathrm{8}=\mathrm{4a}+\mathrm{2b}+\mathrm{c}\left(\mathrm{2}\right)\Rightarrow\begin{cases}{\mathrm{3a}+\mathrm{b}=\mathrm{5}\left(\mathrm{4}\right)}\\{\mathrm{5a}+\mathrm{b}=\mathrm{7}\left(\mathrm{5}\right)}\end{cases}}\\{\mathrm{u}_{\mathrm{3}} =\mathrm{15}=\mathrm{9a}+\mathrm{3b}+\mathrm{c}\left(\mathrm{3}\right)}\end{cases} \\ $$$$\Rightarrow\mathrm{2a}=\mathrm{2}\Rightarrow\mathrm{a}=\mathrm{1}\Rightarrow\mathrm{b}=\mathrm{2},\mathrm{c}=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{u}}_{\boldsymbol{\mathrm{n}}} =\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{n}}\Rightarrow\boldsymbol{\mathrm{u}}_{\mathrm{50}} =\mathrm{50}^{\mathrm{2}} +\mathrm{2}×\mathrm{50}=\mathrm{2600} \\ $$$$\mathrm{S}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\left(\mathrm{k}^{\mathrm{2}} +\mathrm{2k}\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\mathrm{k}^{\mathrm{2}} +\mathrm{2}\underset{\mathrm{l}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\mathrm{k}=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6}}+\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{7}\right)}{\mathrm{6}}.\mathrm{Therefore}, \\ $$$$\boldsymbol{\mathrm{S}}_{\mathrm{50}} =\frac{\mathrm{50}×\mathrm{51}×\mathrm{107}}{\mathrm{6}}=\mathrm{25}×\mathrm{17}×\mathrm{107}=\mathrm{45475} \\ $$$$ \\ $$
Commented by bobhans last updated on 24/Jul/20
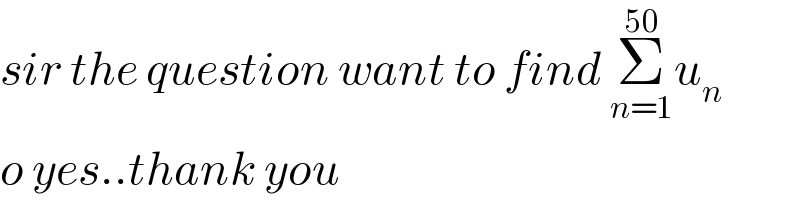
sir the question want to find Σ_(n=1) ^(50) u_n o yes..thank you
$${sir}\:{the}\:{question}\:{want}\:{to}\:{find}\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{50}} {\sum}}{u}_{{n}} \\ $$$${o}\:{yes}..{thank}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *