Question Number 90097 by jagoll last updated on 21/Apr/20
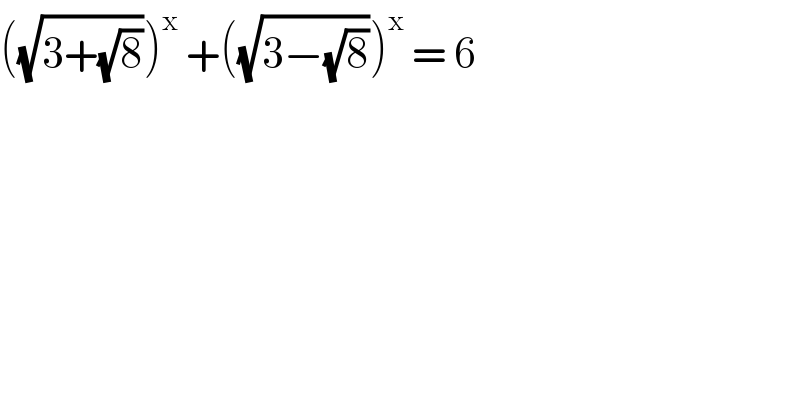
$$\left(\sqrt{\mathrm{3}+\sqrt{\mathrm{8}}}\right)^{\mathrm{x}} \:+\left(\sqrt{\mathrm{3}−\sqrt{\mathrm{8}}}\right)^{\mathrm{x}} \:=\:\mathrm{6} \\ $$
Commented by john santu last updated on 21/Apr/20
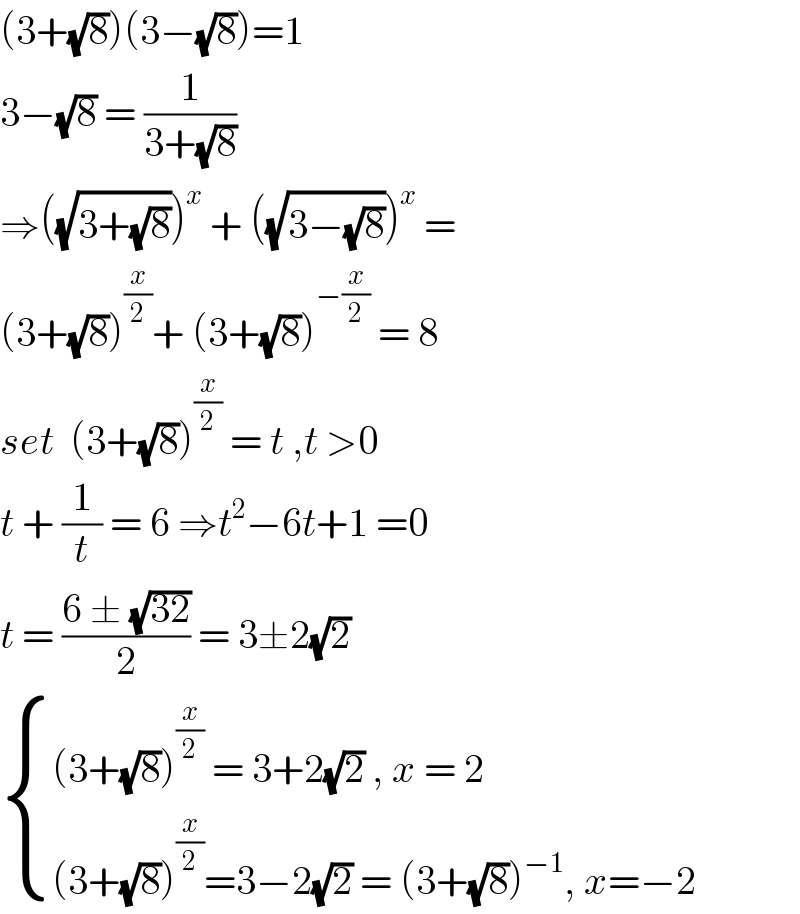
$$\left(\mathrm{3}+\sqrt{\mathrm{8}}\right)\left(\mathrm{3}−\sqrt{\mathrm{8}}\right)=\mathrm{1} \\ $$$$\mathrm{3}−\sqrt{\mathrm{8}}\:=\:\frac{\mathrm{1}}{\mathrm{3}+\sqrt{\mathrm{8}}}\: \\ $$$$\Rightarrow\left(\sqrt{\mathrm{3}+\sqrt{\mathrm{8}}}\right)^{{x}} \:+\:\left(\sqrt{\mathrm{3}−\sqrt{\mathrm{8}}}\right)^{{x}} \:= \\ $$$$\left(\mathrm{3}+\sqrt{\mathrm{8}}\right)^{\frac{{x}}{\mathrm{2}}} +\:\left(\mathrm{3}+\sqrt{\mathrm{8}}\right)^{−\frac{{x}}{\mathrm{2}}} \:=\:\mathrm{8} \\ $$$${set}\:\:\left(\mathrm{3}+\sqrt{\mathrm{8}}\right)^{\frac{{x}}{\mathrm{2}}} \:=\:{t}\:,{t}\:>\mathrm{0} \\ $$$${t}\:+\:\frac{\mathrm{1}}{{t}}\:=\:\mathrm{6}\:\Rightarrow{t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{1}\:=\mathrm{0} \\ $$$${t}\:=\:\frac{\mathrm{6}\:\pm\:\sqrt{\mathrm{32}}}{\mathrm{2}}\:=\:\mathrm{3}\pm\mathrm{2}\sqrt{\mathrm{2}}\: \\ $$$$\begin{cases}{\left(\mathrm{3}+\sqrt{\mathrm{8}}\right)^{\frac{{x}}{\mathrm{2}}} \:=\:\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:,\:{x}\:=\:\mathrm{2}}\\{\left(\mathrm{3}+\sqrt{\mathrm{8}}\right)^{\frac{{x}}{\mathrm{2}}} =\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:=\:\left(\mathrm{3}+\sqrt{\mathrm{8}}\right)^{−\mathrm{1}} ,\:{x}=−\mathrm{2}}\end{cases} \\ $$
