3-cos-x-3-cos-x-dx-

Question Number 167989 by cortano1 last updated on 31/Mar/22

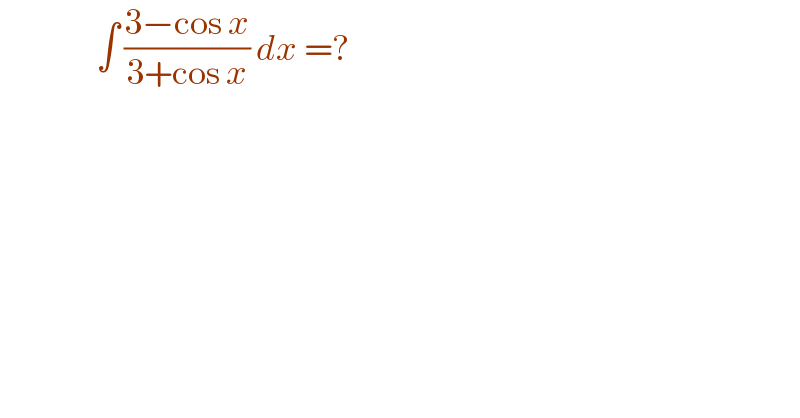
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\:\frac{\mathrm{3}−\mathrm{cos}\:{x}}{\mathrm{3}+\mathrm{cos}\:{x}}\:{dx}\:=? \\ $$

Answered by nimnim last updated on 31/Mar/22

I=∫ ((6−3−cosx)/(3+cosx))dx=∫((6/(3+cosx))−1)dx =6∫(dx/(3+cosx))−∫dx=I_1 −x put t=tan((x/2))⇒ (2/(1+t^2 ))dt=dx sinx=((2t)/(1+t^2 )), cosx=((1−t^2 )/(1+t^2 )) I_1 =6∫(1/(3+((1−t^2 )/(1+t^2 ))))×(2/(1+t^2 ))dt =6∫(2/(4+2t^2 ))dt =6(√2) tan^(−1) ((t/( (√2)))) =6(√2) tan^(−1) ((1/( (√2)))tan((x/2))) I =I_1 −x=6(√2) tan^(−1) ((1/( (√2)))tan((x/2)))−x+C

$$\:\:\mathrm{I}=\int\:\frac{\mathrm{6}−\mathrm{3}−\mathrm{cosx}}{\mathrm{3}+\mathrm{cosx}}\mathrm{dx}=\int\left(\frac{\mathrm{6}}{\mathrm{3}+\mathrm{cosx}}−\mathrm{1}\right)\mathrm{dx} \\ $$$$\:\:\:\:=\mathrm{6}\int\frac{\mathrm{dx}}{\mathrm{3}+\mathrm{cosx}}−\int\mathrm{dx}=\mathrm{I}_{\mathrm{1}} −\mathrm{x} \\ $$$$\:\:\:\:\mathrm{put}\:\mathrm{t}=\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\Rightarrow\:\frac{\mathrm{2}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}=\mathrm{dx} \\ $$$$\:\:\:\:\mathrm{sinx}=\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} },\:\mathrm{cosx}=\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\: \\ $$$$\:\:\mathrm{I}_{\mathrm{1}} =\mathrm{6}\int\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}×\frac{\mathrm{2}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:\:\:\:\:\:=\mathrm{6}\int\frac{\mathrm{2}}{\mathrm{4}+\mathrm{2t}^{\mathrm{2}} }\mathrm{dt}\:=\mathrm{6}\sqrt{\mathrm{2}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{t}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{6}\sqrt{\mathrm{2}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\mathrm{I}\:\:=\mathrm{I}_{\mathrm{1}} −\mathrm{x}=\mathrm{6}\sqrt{\mathrm{2}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)−\mathrm{x}+\mathrm{C} \\ $$

Answered by Florian last updated on 10/Apr/22

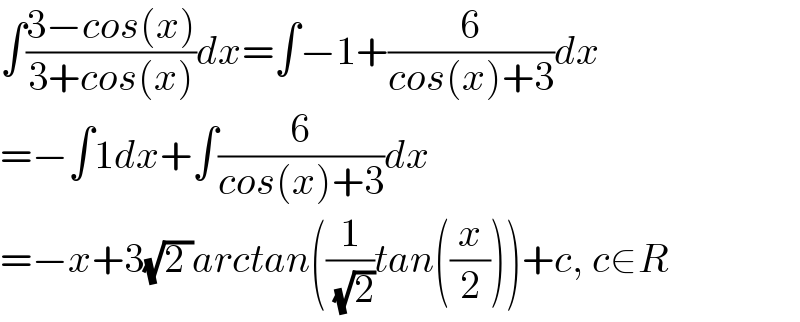
∫((3−cos(x))/(3+cos(x)))dx=∫−1+(6/(cos(x)+3))dx =−∫1dx+∫(6/(cos(x)+3))dx =−x+3(√(2 ))arctan((1/( (√2)))tan((x/2)))+c, c∈R

$$\int\frac{\mathrm{3}−{cos}\left({x}\right)}{\mathrm{3}+{cos}\left({x}\right)}{dx}=\int−\mathrm{1}+\frac{\mathrm{6}}{{cos}\left({x}\right)+\mathrm{3}}{dx} \\ $$$$=−\int\mathrm{1}{dx}+\int\frac{\mathrm{6}}{{cos}\left({x}\right)+\mathrm{3}}{dx} \\ $$$$=−{x}+\mathrm{3}\sqrt{\mathrm{2}\:}{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)+{c},\:{c}\in{R} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply