Question Number 93256 by i jagooll last updated on 12/May/20

$$\begin{cases}{\mathrm{3}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{4}\:\mathrm{cos}\:\mathrm{y}}\\{\mathrm{3}\:\mathrm{sin}\:\mathrm{x}\:+\:\mathrm{4sin}\:\mathrm{y}\:=\:\mathrm{5}}\end{cases} \\ $$$$\mathrm{find}\:\mathrm{x}\:\&\mathrm{y}\:\mathrm{with}\:\mathrm{acute}\:\mathrm{angle}\: \\ $$
Commented by john santu last updated on 12/May/20
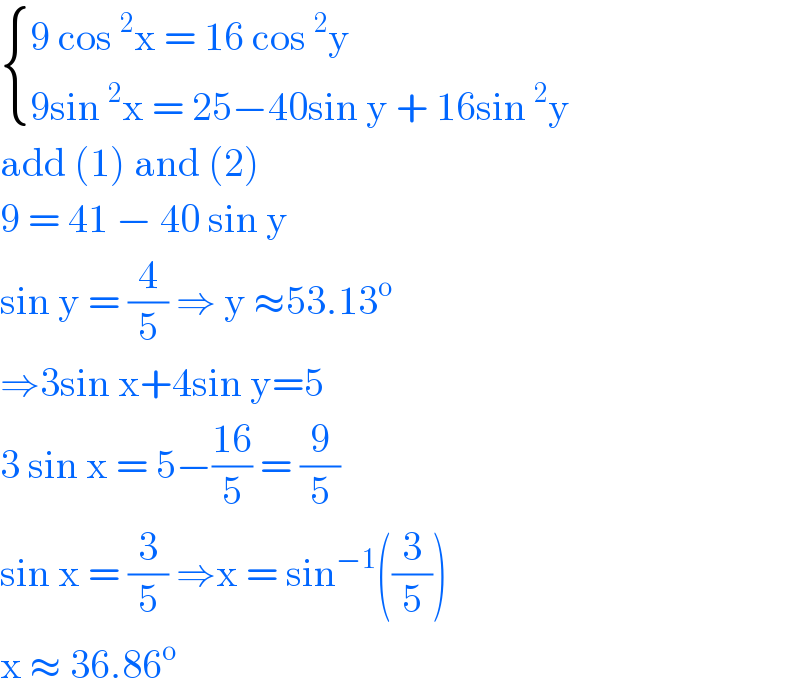
$$\begin{cases}{\mathrm{9}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{16}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{y}}\\{\mathrm{9sin}\:^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{25}−\mathrm{40sin}\:\mathrm{y}\:+\:\mathrm{16sin}\:^{\mathrm{2}} \mathrm{y}}\end{cases} \\ $$$$\mathrm{add}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\: \\ $$$$\mathrm{9}\:=\:\mathrm{41}\:−\:\mathrm{40}\:\mathrm{sin}\:\mathrm{y}\: \\ $$$$\mathrm{sin}\:\mathrm{y}\:=\:\frac{\mathrm{4}}{\mathrm{5}}\:\Rightarrow\:\mathrm{y}\:\approx\mathrm{53}.\mathrm{13}^{\mathrm{o}} \\ $$$$\Rightarrow\mathrm{3sin}\:\mathrm{x}+\mathrm{4sin}\:\mathrm{y}=\mathrm{5} \\ $$$$\mathrm{3}\:\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{5}−\frac{\mathrm{16}}{\mathrm{5}}\:=\:\frac{\mathrm{9}}{\mathrm{5}}\: \\ $$$$\mathrm{sin}\:\mathrm{x}\:=\:\frac{\mathrm{3}}{\mathrm{5}}\:\Rightarrow\mathrm{x}\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{5}}\right) \\ $$$$\mathrm{x}\:\approx\:\mathrm{36}.\mathrm{86}^{\mathrm{o}} \\ $$
Commented by i jagooll last updated on 12/May/20
thank you sir. cooll man ������
