Question Number 14287 by tawa tawa last updated on 30/May/17
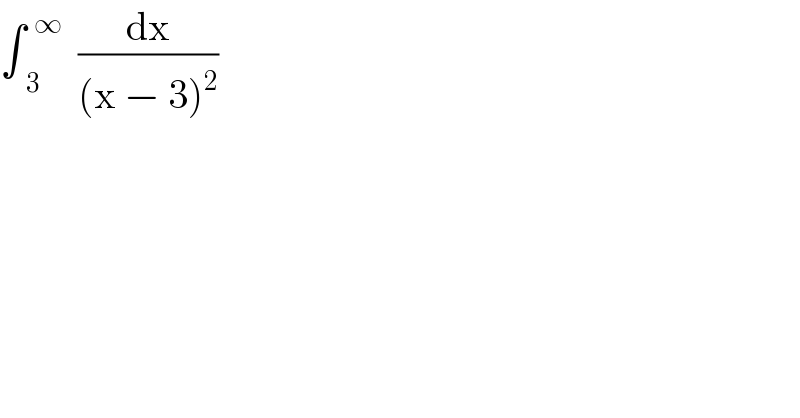
$$\int_{\:\:\mathrm{3}} ^{\:\:\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{x}\:−\:\mathrm{3}\right)^{\mathrm{2}} } \\ $$
Commented by prakash jain last updated on 30/May/17

$$\mathrm{No}\:\mathrm{answer}\:\mathrm{integral}\:\mathrm{does}\:\mathrm{not} \\ $$$$\mathrm{converge}\:\mathrm{so}\:\mathrm{no}\:\mathrm{finite}\:\mathrm{value}. \\ $$$$\mathrm{Maybe}\:\mathrm{u}\:\mathrm{can}\:\mathrm{say}\:\infty. \\ $$
Commented by Tinkutara last updated on 30/May/17

$$\mathrm{So}\:\mathrm{what}\:\mathrm{will}\:\mathrm{be}\:\mathrm{the}\:\mathrm{answer}?\:\mathrm{I}\:\mathrm{was} \\ $$$$\mathrm{thinking}\:\mathrm{mine}\:\mathrm{was}\:\mathrm{wrong}. \\ $$
Commented by Tinkutara last updated on 30/May/17
![∫_3 ^∞ (dx/((x − 3)^2 )) = −[(1/(x − 3))]_3 ^∞ = −[(1/∞) − (1/∞)] = 0](https://www.tinkutara.com/question/Q14289.png)
$$\int_{\mathrm{3}} ^{\infty} \frac{{dx}}{\left({x}\:−\:\mathrm{3}\right)^{\mathrm{2}} }\:=\:−\left[\frac{\mathrm{1}}{{x}\:−\:\mathrm{3}}\right]_{\mathrm{3}} ^{\infty} \\ $$$$=\:−\left[\frac{\mathrm{1}}{\infty}\:−\:\frac{\mathrm{1}}{\infty}\right]\:=\:\mathrm{0} \\ $$
Commented by tawa tawa last updated on 30/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$$$ \\ $$
Commented by prakash jain last updated on 30/May/17
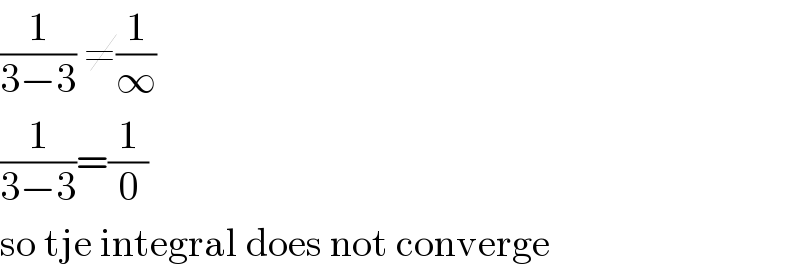
$$\frac{\mathrm{1}}{\mathrm{3}−\mathrm{3}}\:\neq\frac{\mathrm{1}}{\infty} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}−\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{0}} \\ $$$$\mathrm{so}\:\mathrm{tje}\:\mathrm{integral}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge} \\ $$
