Menu Close

3-sin3x-cos3x-2sin-9x-4-2-

Tinku Tara 0 Comments
Pin




Question Number 41878 by lucha116 last updated on 14/Aug/18
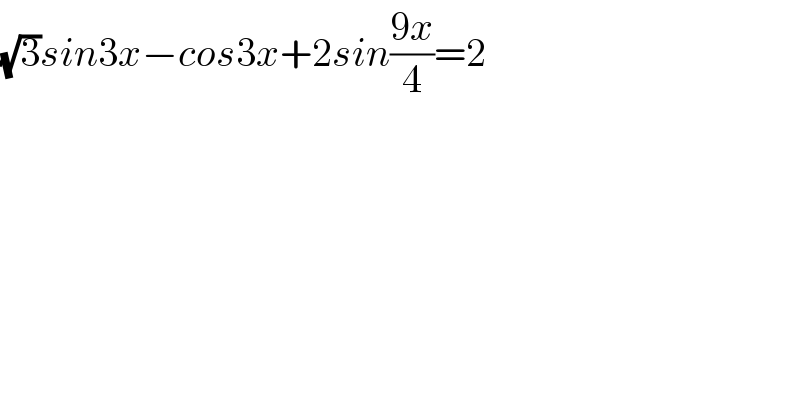
(√3)sin3x−cos3x+2sin((9x)/4)=2
$$\sqrt{\mathrm{3}}{sin}\mathrm{3}{x}−{cos}\mathrm{3}{x}+\mathrm{2}{sin}\frac{\mathrm{9}{x}}{\mathrm{4}}=\mathrm{2} \\ $$
Answered by MJS last updated on 15/Aug/18
f(x)=(√3)sin 3x −cos 3x +2sin ((9x)/4) −2 found by approximation: max(f(x))= (((((2π)/9)+((8π)/3)n)),(2) ) with n∈Z ⇒ period length = ((8π)/3) shift ((2π)/9) to the left to get it symmetric to x=0 x=r+((2π)/9) f(r)=(√3)sin (3r+((2π)/3))−cos (3r+((2π)/3)) +2sin (((9r)/4)+(π/2)) −2 f(r)=2(cos 3r +cos ((9r)/4) −1) s=((4r)/3) f(s)=2(cos 4s +cos 3s −1) cos 4s +cos 3s −1=0 s=(π/2)+πz ⇒ x=((8π)/9)+((4π)/3)z approximately s≈.297356+2πz ⇒ x≈1.09461+((8π)/3)z s≈1.93560+2πz ⇒ x≈3.27894+((8π)/3)z (z∈Z) exactly cos 4s +cos 3s −1=0 s=2arctan t ⇒ (t−1)(t+1)(t^6 +19t^4 −45t^2 +1)=0 t=±1 ⇒ s=±(π/2) t^6 +19t^4 −45t^2 +1=0 this is symm. to x=0, we only need positive solutions t=(√u) u^3 +19u^2 −45u+1=0 u=v−((19)/3) v^3 −((496)/3)v+((21440)/(27))=0 trigonometric method gives v_1 =((8(√(31)))/3)sin (((arcsin (((335(√(31)))/(1922))))/3)) v_2 =((8(√(31)))/3)cos (((arcsin (((335(√(31)))/(1922))))/3)+(π/6)) v_3 =−((8(√(31)))/3)sin (((arcsin (((335(√(31)))/(1922))))/3)+(π/3)) <0 ⇒ not useable these cannot be further simplfied, so we again have to approximate going back all the way gives the same solutiond as above
$${f}\left({x}\right)=\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{3}{x}\:−\mathrm{cos}\:\mathrm{3}{x}\:+\mathrm{2sin}\:\frac{\mathrm{9}{x}}{\mathrm{4}}\:−\mathrm{2} \\ $$$$\mathrm{found}\:\mathrm{by}\:\mathrm{approximation}: \\ $$$$\mathrm{max}\left({f}\left({x}\right)\right)=\begin{pmatrix}{\frac{\mathrm{2}\pi}{\mathrm{9}}+\frac{\mathrm{8}\pi}{\mathrm{3}}{n}}\\{\mathrm{2}}\end{pmatrix}\:\mathrm{with}\:{n}\in\mathbb{Z} \\ $$$$\Rightarrow\:\mathrm{period}\:\mathrm{length}\:=\:\frac{\mathrm{8}\pi}{\mathrm{3}} \\ $$$$\mathrm{shift}\:\frac{\mathrm{2}\pi}{\mathrm{9}}\:\mathrm{to}\:\mathrm{the}\:\mathrm{left}\:\mathrm{to}\:\mathrm{get}\:\mathrm{it}\:\mathrm{symmetric}\:\mathrm{to}\:{x}=\mathrm{0} \\ $$$${x}={r}+\frac{\mathrm{2}\pi}{\mathrm{9}} \\ $$$${f}\left({r}\right)=\sqrt{\mathrm{3}}\mathrm{sin}\:\left(\mathrm{3}{r}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)−\mathrm{cos}\:\left(\mathrm{3}{r}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\:+\mathrm{2sin}\:\left(\frac{\mathrm{9}{r}}{\mathrm{4}}+\frac{\pi}{\mathrm{2}}\right)\:−\mathrm{2} \\ $$$${f}\left({r}\right)=\mathrm{2}\left(\mathrm{cos}\:\mathrm{3}{r}\:+\mathrm{cos}\:\frac{\mathrm{9}{r}}{\mathrm{4}}\:−\mathrm{1}\right) \\ $$$${s}=\frac{\mathrm{4}{r}}{\mathrm{3}} \\ $$$${f}\left({s}\right)=\mathrm{2}\left(\mathrm{cos}\:\mathrm{4}{s}\:+\mathrm{cos}\:\mathrm{3}{s}\:−\mathrm{1}\right) \\ $$$$\mathrm{cos}\:\mathrm{4}{s}\:+\mathrm{cos}\:\mathrm{3}{s}\:−\mathrm{1}=\mathrm{0} \\ $$$${s}=\frac{\pi}{\mathrm{2}}+\pi{z}\:\Rightarrow\:{x}=\frac{\mathrm{8}\pi}{\mathrm{9}}+\frac{\mathrm{4}\pi}{\mathrm{3}}{z} \\ $$$$\mathrm{approximately} \\ $$$${s}\approx.\mathrm{297356}+\mathrm{2}\pi{z}\:\Rightarrow\:{x}\approx\mathrm{1}.\mathrm{09461}+\frac{\mathrm{8}\pi}{\mathrm{3}}{z} \\ $$$${s}\approx\mathrm{1}.\mathrm{93560}+\mathrm{2}\pi{z}\:\Rightarrow\:{x}\approx\mathrm{3}.\mathrm{27894}+\frac{\mathrm{8}\pi}{\mathrm{3}}{z} \\ $$$$\left({z}\in\mathbb{Z}\right) \\ $$$$\mathrm{exactly} \\ $$$$\mathrm{cos}\:\mathrm{4}{s}\:+\mathrm{cos}\:\mathrm{3}{s}\:−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{s}=\mathrm{2arctan}\:{t} \\ $$$$\Rightarrow\:\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{6}} +\mathrm{19}{t}^{\mathrm{4}} −\mathrm{45}{t}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$${t}=\pm\mathrm{1}\:\Rightarrow\:{s}=\pm\frac{\pi}{\mathrm{2}} \\ $$$${t}^{\mathrm{6}} +\mathrm{19}{t}^{\mathrm{4}} −\mathrm{45}{t}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{symm}.\:\mathrm{to}\:{x}=\mathrm{0},\:\mathrm{we}\:\mathrm{only}\:\mathrm{need}\:\mathrm{positive} \\ $$$$\mathrm{solutions} \\ $$$${t}=\sqrt{{u}} \\ $$$${u}^{\mathrm{3}} +\mathrm{19}{u}^{\mathrm{2}} −\mathrm{45}{u}+\mathrm{1}=\mathrm{0} \\ $$$${u}={v}−\frac{\mathrm{19}}{\mathrm{3}} \\ $$$${v}^{\mathrm{3}} −\frac{\mathrm{496}}{\mathrm{3}}{v}+\frac{\mathrm{21440}}{\mathrm{27}}=\mathrm{0} \\ $$$$\mathrm{trigonometric}\:\mathrm{method}\:\mathrm{gives} \\ $$$${v}_{\mathrm{1}} =\frac{\mathrm{8}\sqrt{\mathrm{31}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{arcsin}\:\left(\frac{\mathrm{335}\sqrt{\mathrm{31}}}{\mathrm{1922}}\right)}{\mathrm{3}}\right) \\ $$$${v}_{\mathrm{2}} =\frac{\mathrm{8}\sqrt{\mathrm{31}}}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\mathrm{arcsin}\:\left(\frac{\mathrm{335}\sqrt{\mathrm{31}}}{\mathrm{1922}}\right)}{\mathrm{3}}+\frac{\pi}{\mathrm{6}}\right) \\ $$$${v}_{\mathrm{3}} =−\frac{\mathrm{8}\sqrt{\mathrm{31}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{arcsin}\:\left(\frac{\mathrm{335}\sqrt{\mathrm{31}}}{\mathrm{1922}}\right)}{\mathrm{3}}+\frac{\pi}{\mathrm{3}}\right)\:<\mathrm{0}\:\Rightarrow\:\mathrm{not}\:\mathrm{useable} \\ $$$$\mathrm{these}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{further}\:\mathrm{simplfied},\:\mathrm{so}\:\mathrm{we}\:\mathrm{again} \\ $$$$\mathrm{have}\:\mathrm{to}\:\mathrm{approximate} \\ $$$$\mathrm{going}\:\mathrm{back}\:\mathrm{all}\:\mathrm{the}\:\mathrm{way}\:\mathrm{gives}\:\mathrm{the}\:\mathrm{same}\:\mathrm{solutiond} \\ $$$$\mathrm{as}\:\mathrm{above} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *