Menu Close

3-sin3x-cos3x-2sin-9x-4-4-

Tinku Tara 0 Comments
Pin




Question Number 41895 by lucha116 last updated on 15/Aug/18
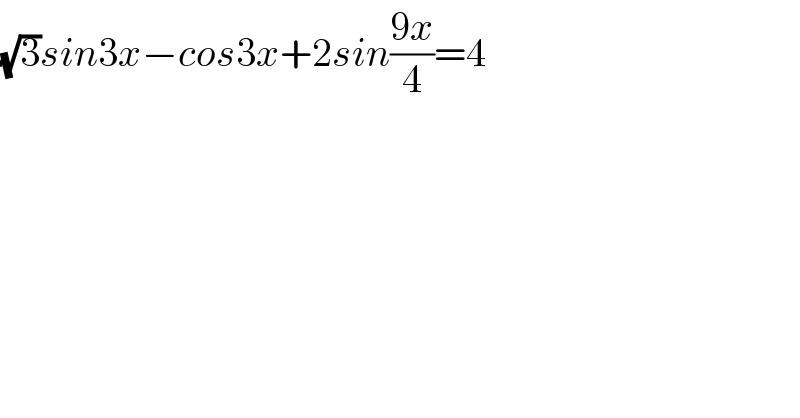
(√3)sin3x−cos3x+2sin((9x)/4)=4
$$\sqrt{\mathrm{3}}{sin}\mathrm{3}{x}−{cos}\mathrm{3}{x}+\mathrm{2}{sin}\frac{\mathrm{9}{x}}{\mathrm{4}}=\mathrm{4} \\ $$
Commented by MJS last updated on 15/Aug/18
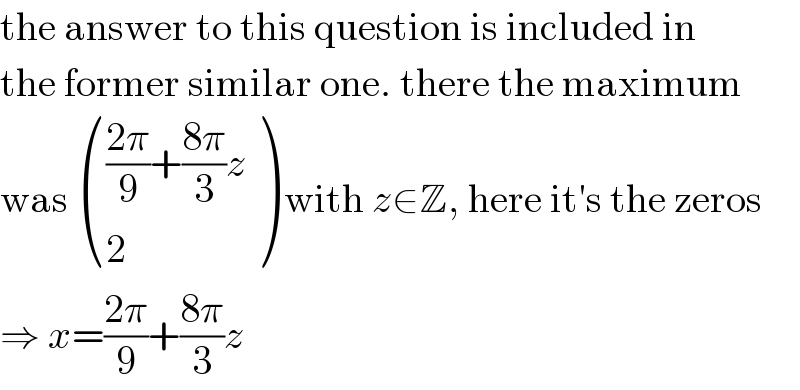
the answer to this question is included in the former similar one. there the maximum was (((((2π)/9)+((8π)/3)z)),(2) ) with z∈Z, here it′s the zeros ⇒ x=((2π)/9)+((8π)/3)z
$$\mathrm{the}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{this}\:\mathrm{question}\:\mathrm{is}\:\mathrm{included}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{former}\:\mathrm{similar}\:\mathrm{one}.\:\mathrm{there}\:\mathrm{the}\:\mathrm{maximum} \\ $$$$\mathrm{was}\:\begin{pmatrix}{\frac{\mathrm{2}\pi}{\mathrm{9}}+\frac{\mathrm{8}\pi}{\mathrm{3}}{z}}\\{\mathrm{2}}\end{pmatrix}\:\mathrm{with}\:{z}\in\mathbb{Z},\:\mathrm{here}\:\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{zeros} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{2}\pi}{\mathrm{9}}+\frac{\mathrm{8}\pi}{\mathrm{3}}{z} \\ $$
Answered by MrW3 last updated on 15/Aug/18
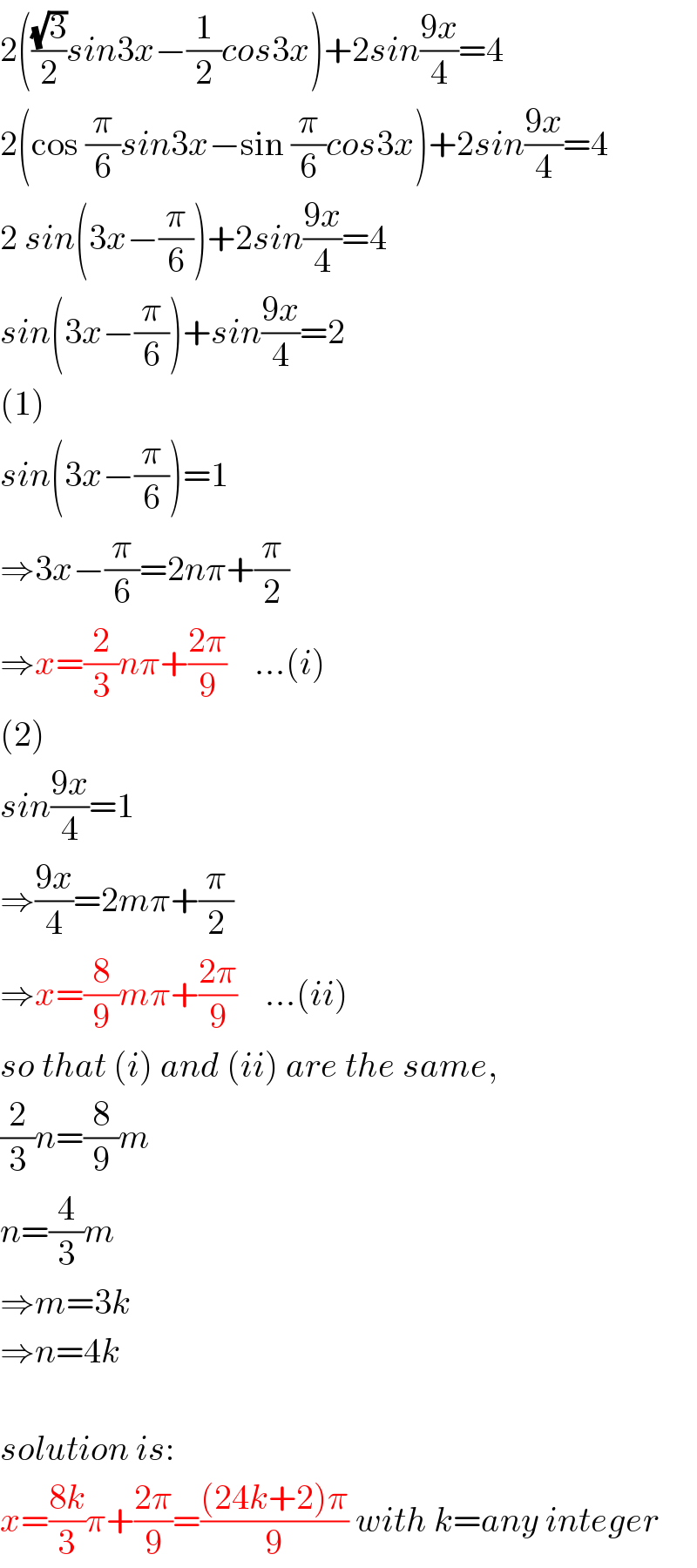
2(((√3)/2)sin3x−(1/2)cos3x)+2sin((9x)/4)=4 2(cos (π/6)sin3x−sin (π/6)cos3x)+2sin((9x)/4)=4 2 sin(3x−(π/6))+2sin((9x)/4)=4 sin(3x−(π/6))+sin((9x)/4)=2 (1) sin(3x−(π/6))=1 ⇒3x−(π/6)=2nπ+(π/2) ⇒x=(2/3)nπ+((2π)/9) ...(i) (2) sin((9x)/4)=1 ⇒((9x)/4)=2mπ+(π/2) ⇒x=(8/9)mπ+((2π)/9) ...(ii) so that (i) and (ii) are the same, (2/3)n=(8/9)m n=(4/3)m ⇒m=3k ⇒n=4k solution is: x=((8k)/3)π+((2π)/9)=(((24k+2)π)/9) with k=any integer
$$\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sin}\mathrm{3}{x}−\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{3}{x}\right)+\mathrm{2}{sin}\frac{\mathrm{9}{x}}{\mathrm{4}}=\mathrm{4} \\ $$$$\mathrm{2}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{6}}{sin}\mathrm{3}{x}−\mathrm{sin}\:\frac{\pi}{\mathrm{6}}{cos}\mathrm{3}{x}\right)+\mathrm{2}{sin}\frac{\mathrm{9}{x}}{\mathrm{4}}=\mathrm{4} \\ $$$$\mathrm{2}\:{sin}\left(\mathrm{3}{x}−\frac{\pi}{\mathrm{6}}\right)+\mathrm{2}{sin}\frac{\mathrm{9}{x}}{\mathrm{4}}=\mathrm{4} \\ $$$${sin}\left(\mathrm{3}{x}−\frac{\pi}{\mathrm{6}}\right)+{sin}\frac{\mathrm{9}{x}}{\mathrm{4}}=\mathrm{2} \\ $$$$\left(\mathrm{1}\right) \\ $$$${sin}\left(\mathrm{3}{x}−\frac{\pi}{\mathrm{6}}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}{x}−\frac{\pi}{\mathrm{6}}=\mathrm{2}{n}\pi+\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}}{\mathrm{3}}{n}\pi+\frac{\mathrm{2}\pi}{\mathrm{9}}\:\:\:\:…\left({i}\right) \\ $$$$\left(\mathrm{2}\right) \\ $$$${sin}\frac{\mathrm{9}{x}}{\mathrm{4}}=\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{9}{x}}{\mathrm{4}}=\mathrm{2}{m}\pi+\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{8}}{\mathrm{9}}{m}\pi+\frac{\mathrm{2}\pi}{\mathrm{9}}\:\:\:\:…\left({ii}\right) \\ $$$${so}\:{that}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{are}\:{the}\:{same}, \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}{n}=\frac{\mathrm{8}}{\mathrm{9}}{m} \\ $$$${n}=\frac{\mathrm{4}}{\mathrm{3}}{m} \\ $$$$\Rightarrow{m}=\mathrm{3}{k} \\ $$$$\Rightarrow{n}=\mathrm{4}{k} \\ $$$$ \\ $$$${solution}\:{is}: \\ $$$${x}=\frac{\mathrm{8}{k}}{\mathrm{3}}\pi+\frac{\mathrm{2}\pi}{\mathrm{9}}=\frac{\left(\mathrm{24}{k}+\mathrm{2}\right)\pi}{\mathrm{9}}\:{with}\:{k}={any}\:{integer} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *