Question Number 24866 by kosarrr last updated on 27/Nov/17
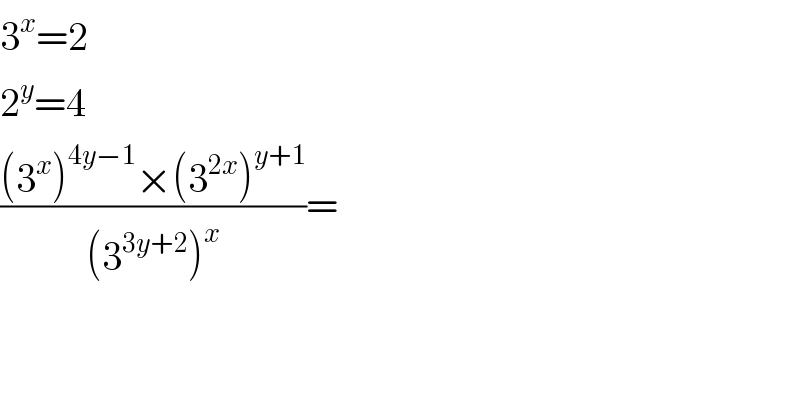
$$\mathrm{3}^{{x}} =\mathrm{2} \\ $$$$\mathrm{2}^{{y}} =\mathrm{4} \\ $$$$\frac{\left(\mathrm{3}^{{x}} \right)^{\mathrm{4}{y}−\mathrm{1}} ×\left(\mathrm{3}^{\mathrm{2}{x}} \right)^{{y}+\mathrm{1}} }{\left(\mathrm{3}^{\mathrm{3}{y}+\mathrm{2}} \right)^{{x}} }= \\ $$
Answered by jota+ last updated on 27/Nov/17
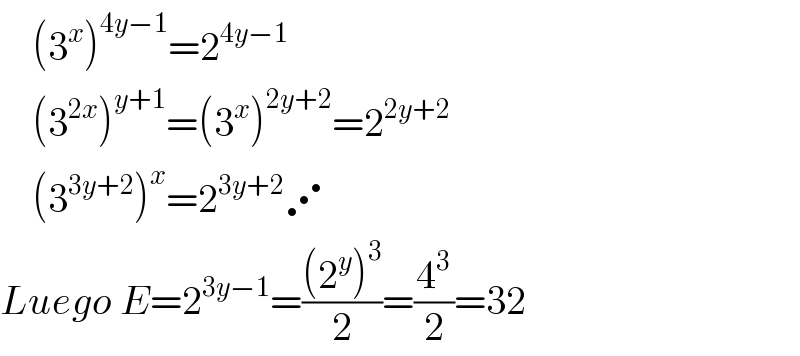
$$\:\:\:\:\left(\mathrm{3}^{{x}} \right)^{\mathrm{4}{y}−\mathrm{1}} =\mathrm{2}^{\mathrm{4}{y}−\mathrm{1}} \\ $$$$\:\:\:\:\left(\mathrm{3}^{\mathrm{2}{x}} \right)^{{y}+\mathrm{1}} =\left(\mathrm{3}^{{x}} \right)^{\mathrm{2}{y}+\mathrm{2}} =\mathrm{2}^{\mathrm{2}{y}+\mathrm{2}} \\ $$$$\:\:\:\:\left(\mathrm{3}^{\mathrm{3}{y}+\mathrm{2}} \right)^{{x}} =\mathrm{2}^{\mathrm{3}{y}+\mathrm{2}} \iddots \\ $$$${Luego}\:{E}=\mathrm{2}^{\mathrm{3}{y}−\mathrm{1}} =\frac{\left(\mathrm{2}^{{y}} \right)^{\mathrm{3}} }{\mathrm{2}}=\frac{\mathrm{4}^{\mathrm{3}} }{\mathrm{2}}=\mathrm{32} \\ $$
Answered by Rasheed.Sindhi last updated on 29/Nov/17
![2^y =4=2^2 ⇒y=2 (((3^x )^(4y−1) ×(3^(2x) )^(y+1) )/((3^(3y+2) )^x )) =(((3^x )^(4y−1) ×(3^x )^(2(y+1)) )/((3^x )^(3y+2) )) =(((2)^(4(2)−1) ×(2)^(2(2+1)) )/((2)^(3(2)+2) ))[∵3^x =2,y=2] =((2^7 ×2^6 )/2^8 )=2^5 =32](https://www.tinkutara.com/question/Q24901.png)
$$\mathrm{2}^{{y}} =\mathrm{4}=\mathrm{2}^{\mathrm{2}} \Rightarrow{y}=\mathrm{2} \\ $$$$\frac{\left(\mathrm{3}^{{x}} \right)^{\mathrm{4}{y}−\mathrm{1}} ×\left(\mathrm{3}^{\mathrm{2}{x}} \right)^{{y}+\mathrm{1}} }{\left(\mathrm{3}^{\mathrm{3}{y}+\mathrm{2}} \right)^{{x}} } \\ $$$$=\frac{\left(\mathrm{3}^{{x}} \right)^{\mathrm{4}{y}−\mathrm{1}} ×\left(\mathrm{3}^{{x}} \right)^{\mathrm{2}\left({y}+\mathrm{1}\right)} }{\left(\mathrm{3}^{{x}} \right)^{\mathrm{3}{y}+\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{2}\right)^{\mathrm{4}\left(\mathrm{2}\right)−\mathrm{1}} ×\left(\mathrm{2}\right)^{\mathrm{2}\left(\mathrm{2}+\mathrm{1}\right)} }{\left(\mathrm{2}\right)^{\mathrm{3}\left(\mathrm{2}\right)+\mathrm{2}} }\left[\because\mathrm{3}^{{x}} =\mathrm{2},{y}=\mathrm{2}\right] \\ $$$$=\frac{\mathrm{2}^{\mathrm{7}} ×\mathrm{2}^{\mathrm{6}} }{\mathrm{2}^{\mathrm{8}} }=\mathrm{2}^{\mathrm{5}} =\mathrm{32} \\ $$
