Question Number 88873 by jagoll last updated on 13/Apr/20
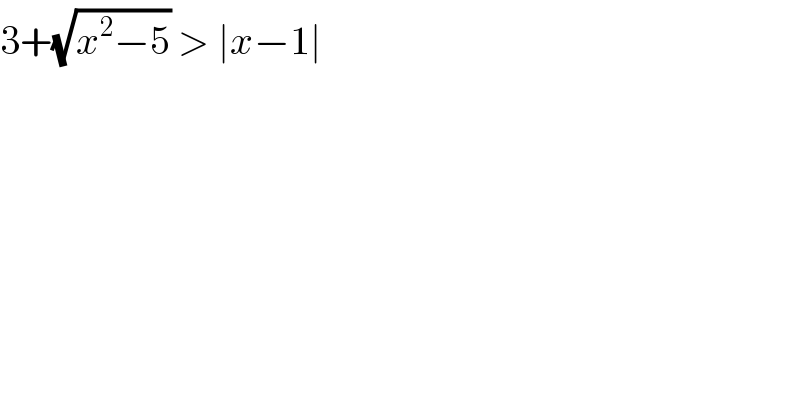
$$\mathrm{3}+\sqrt{{x}^{\mathrm{2}} −\mathrm{5}}\:>\:\mid{x}−\mathrm{1}\mid\: \\ $$
Commented by john santu last updated on 13/Apr/20
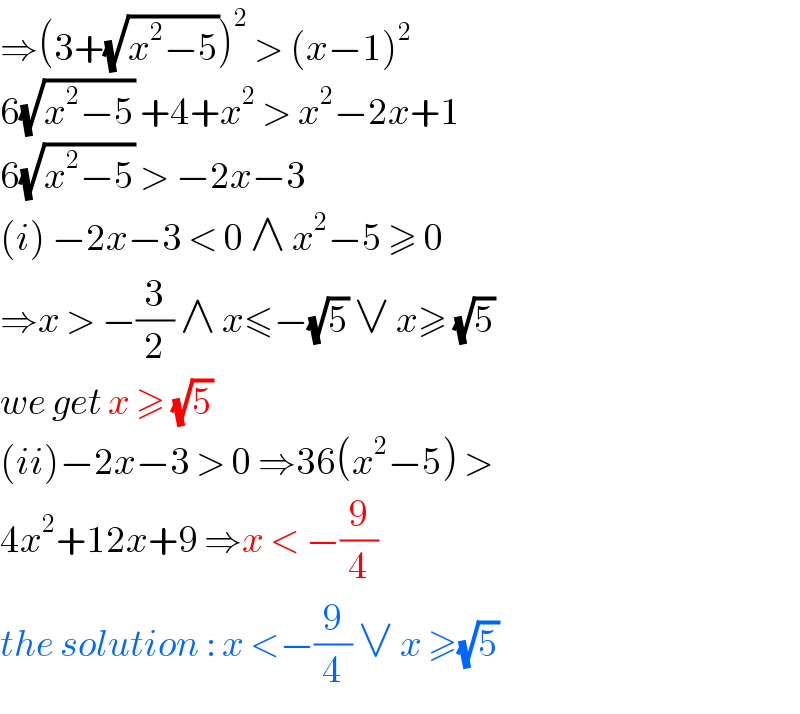
$$\Rightarrow\left(\mathrm{3}+\sqrt{{x}^{\mathrm{2}} −\mathrm{5}}\right)^{\mathrm{2}} \:>\:\left({x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{6}\sqrt{{x}^{\mathrm{2}} −\mathrm{5}}\:+\mathrm{4}+{x}^{\mathrm{2}} \:>\:{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1} \\ $$$$\mathrm{6}\sqrt{{x}^{\mathrm{2}} −\mathrm{5}}\:>\:−\mathrm{2}{x}−\mathrm{3}\: \\ $$$$\left({i}\right)\:−\mathrm{2}{x}−\mathrm{3}\:<\:\mathrm{0}\:\wedge\:{x}^{\mathrm{2}} −\mathrm{5}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow{x}\:>\:−\frac{\mathrm{3}}{\mathrm{2}}\:\wedge\:{x}\leqslant−\sqrt{\mathrm{5}}\:\vee\:{x}\geqslant\:\sqrt{\mathrm{5}} \\ $$$${we}\:{get}\:{x}\:\geqslant\:\sqrt{\mathrm{5}}\: \\ $$$$\left({ii}\right)−\mathrm{2}{x}−\mathrm{3}\:>\:\mathrm{0}\:\Rightarrow\mathrm{36}\left({x}^{\mathrm{2}} −\mathrm{5}\right)\:> \\ $$$$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{9}\:\Rightarrow{x}\:<\:−\frac{\mathrm{9}}{\mathrm{4}} \\ $$$${the}\:{solution}\::\:{x}\:<−\frac{\mathrm{9}}{\mathrm{4}}\:\vee\:{x}\:\geqslant\sqrt{\mathrm{5}}\: \\ $$
