Question Number 157637 by quvonch3737 last updated on 25/Oct/21

$$\:\:\:\:\:\:\mathrm{3}^{{x}} =\mathrm{2}^{{x}} {y}+\mathrm{1} \\ $$$$\:\:\:\:\:\left\{\boldsymbol{{x}}:\boldsymbol{{y}}\right\}\:\varepsilon\mathbb{N}.\: \\ $$
Answered by MathsFan last updated on 25/Oct/21

$$\mathrm{3}^{{x}} −\mathrm{2}^{{x}} {y}=\mathrm{1} \\ $$$$\mathrm{3}^{{x}} −\mathrm{2}^{{x}} {y}=\mathrm{3}−\mathrm{2} \\ $$$${by}\:{comparison} \\ $$$$\:\begin{cases}{\mathrm{3}^{{x}} =\mathrm{3}\:\:\Rightarrow\:{x}=\mathrm{1}}\\{\mathrm{2}^{{x}} {y}=\mathrm{2}\:\Rightarrow\:{y}=\mathrm{1}}\end{cases} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Oct/21
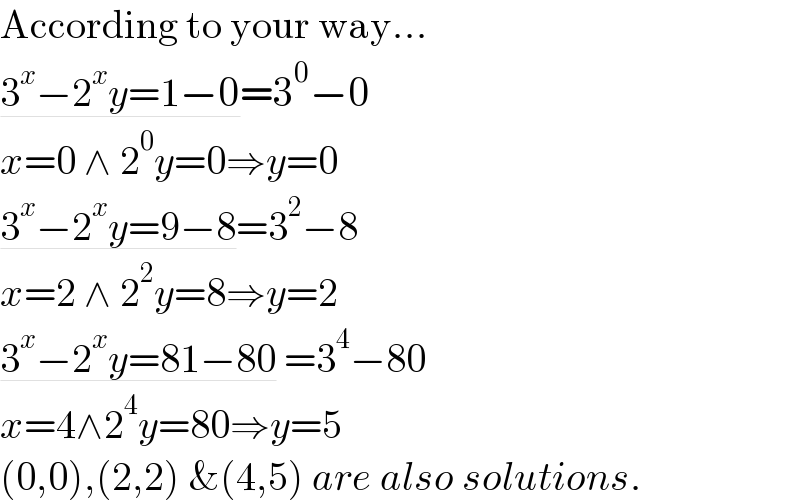
$$\mathrm{According}\:\mathrm{to}\:\mathrm{your}\:\mathrm{way}… \\ $$$$\underline{\mathrm{3}^{{x}} −\mathrm{2}^{{x}} {y}=\mathrm{1}−\mathrm{0}}=\mathrm{3}^{\mathrm{0}} −\mathrm{0} \\ $$$${x}=\mathrm{0}\:\wedge\:\mathrm{2}^{\mathrm{0}} {y}=\mathrm{0}\Rightarrow{y}=\mathrm{0} \\ $$$$\underline{\mathrm{3}^{{x}} −\mathrm{2}^{{x}} {y}=\mathrm{9}−\mathrm{8}}=\mathrm{3}^{\mathrm{2}} −\mathrm{8} \\ $$$${x}=\mathrm{2}\:\wedge\:\mathrm{2}^{\mathrm{2}} {y}=\mathrm{8}\Rightarrow{y}=\mathrm{2} \\ $$$$\underline{\mathrm{3}^{{x}} −\mathrm{2}^{{x}} {y}=\mathrm{81}−\mathrm{80}}\:=\mathrm{3}^{\mathrm{4}} −\mathrm{80} \\ $$$${x}=\mathrm{4}\wedge\mathrm{2}^{\mathrm{4}} {y}=\mathrm{80}\Rightarrow{y}=\mathrm{5} \\ $$$$\left(\mathrm{0},\mathrm{0}\right),\left(\mathrm{2},\mathrm{2}\right)\:\&\left(\mathrm{4},\mathrm{5}\right)\:{are}\:{also}\:{solutions}. \\ $$
Commented by MathsFan last updated on 26/Oct/21

$${thanks}\:{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Oct/21

$${You}'{re}\:{welcome}! \\ $$
Answered by Rasheed.Sindhi last updated on 26/Oct/21
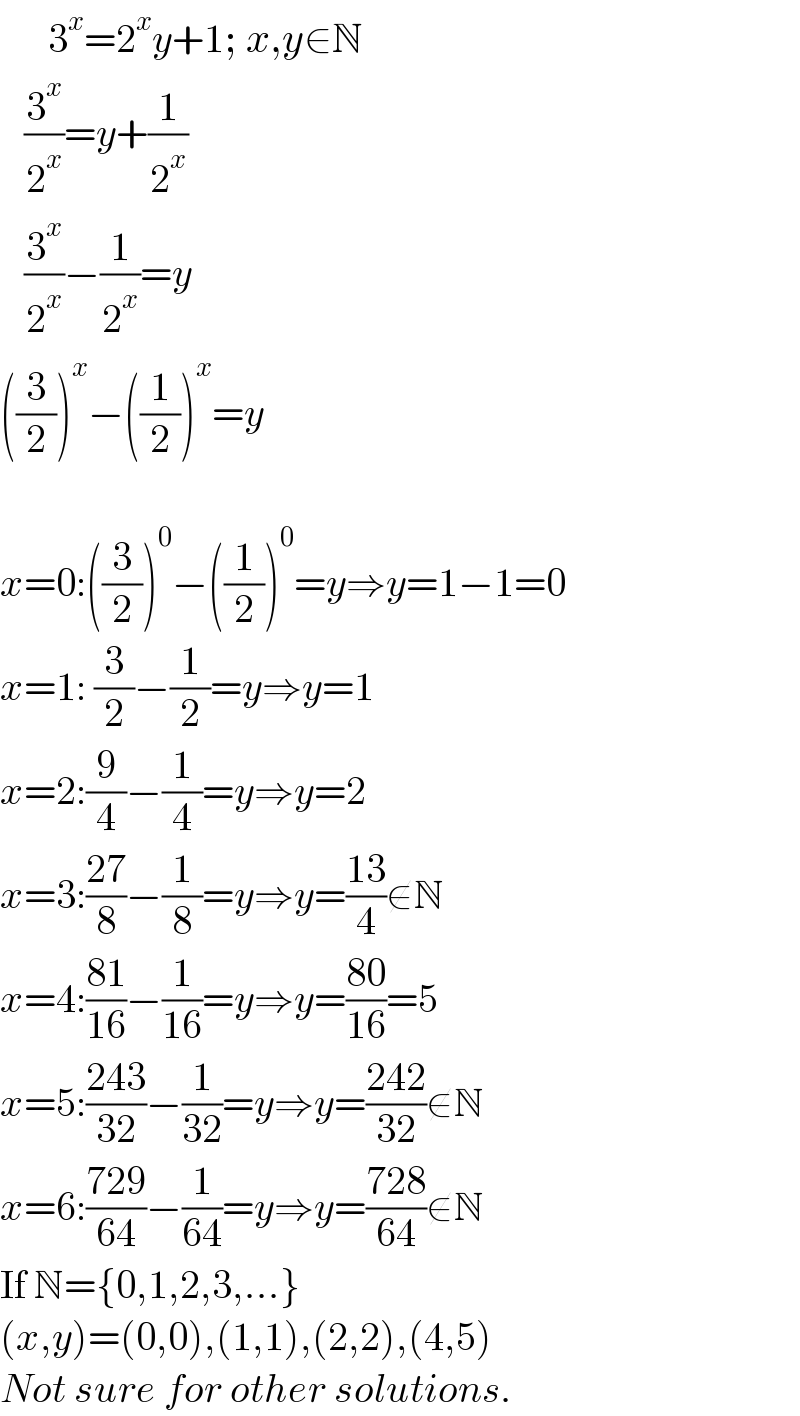
$$\:\:\:\:\:\:\mathrm{3}^{{x}} =\mathrm{2}^{{x}} {y}+\mathrm{1};\:{x},{y}\in\mathbb{N} \\ $$$$\:\:\:\frac{\mathrm{3}^{{x}} }{\mathrm{2}^{{x}} }={y}+\frac{\mathrm{1}}{\mathrm{2}^{{x}} } \\ $$$$\:\:\:\frac{\mathrm{3}^{{x}} }{\mathrm{2}^{{x}} }−\frac{\mathrm{1}}{\mathrm{2}^{{x}} }={y} \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{x}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} ={y} \\ $$$$ \\ $$$${x}=\mathrm{0}:\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{0}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{0}} ={y}\Rightarrow{y}=\mathrm{1}−\mathrm{1}=\mathrm{0} \\ $$$${x}=\mathrm{1}:\:\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}={y}\Rightarrow{y}=\mathrm{1} \\ $$$${x}=\mathrm{2}:\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}={y}\Rightarrow{y}=\mathrm{2} \\ $$$${x}=\mathrm{3}:\frac{\mathrm{27}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}}={y}\Rightarrow{y}=\frac{\mathrm{13}}{\mathrm{4}}\notin\mathbb{N} \\ $$$${x}=\mathrm{4}:\frac{\mathrm{81}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{16}}={y}\Rightarrow{y}=\frac{\mathrm{80}}{\mathrm{16}}=\mathrm{5} \\ $$$${x}=\mathrm{5}:\frac{\mathrm{243}}{\mathrm{32}}−\frac{\mathrm{1}}{\mathrm{32}}={y}\Rightarrow{y}=\frac{\mathrm{242}}{\mathrm{32}}\notin\mathbb{N} \\ $$$${x}=\mathrm{6}:\frac{\mathrm{729}}{\mathrm{64}}−\frac{\mathrm{1}}{\mathrm{64}}={y}\Rightarrow{y}=\frac{\mathrm{728}}{\mathrm{64}}\notin\mathbb{N} \\ $$$$\mathrm{If}\:\mathbb{N}=\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},…\right\} \\ $$$$\left({x},{y}\right)=\left(\mathrm{0},\mathrm{0}\right),\left(\mathrm{1},\mathrm{1}\right),\left(\mathrm{2},\mathrm{2}\right),\left(\mathrm{4},\mathrm{5}\right) \\ $$$${Not}\:{sure}\:{for}\:{other}\:{solutions}. \\ $$
